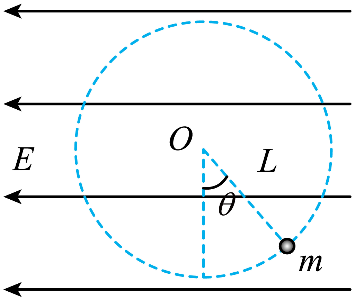
如图所示，在竖直平面内有水平向左的匀强电场，在匀强电场中有一根长为$L$的绝缘细线，细线一端固定在$O$点，另一端系一质量为$m$的带电小球。小球静止时细线与竖直方向成$\theta$角，此时让小球获得初速度且恰能绕$O$点在竖直平面内沿逆时针方向做圆周运动，重力加速度为$g$，不考虑空气阻力。下列说法正确的是$(\qquad)$

匀强电场的电场强度$E=\\dfrac{mg\\tan\\theta}{q}$

小球做圆周运动过程中动能的最小值为$E_{\\text{k}\\min}=\\dfrac{mgL}{2\\sin\\theta}$

小球运动至圆周轨迹的最高点时机械能最小

小球从初始位置开始，在竖直平面内运动一周的过程中，其电势能先减小后增大

$\rm A$．小球静止时细线与竖直方向成$\theta$角，对小球进行受力分析，如图所示

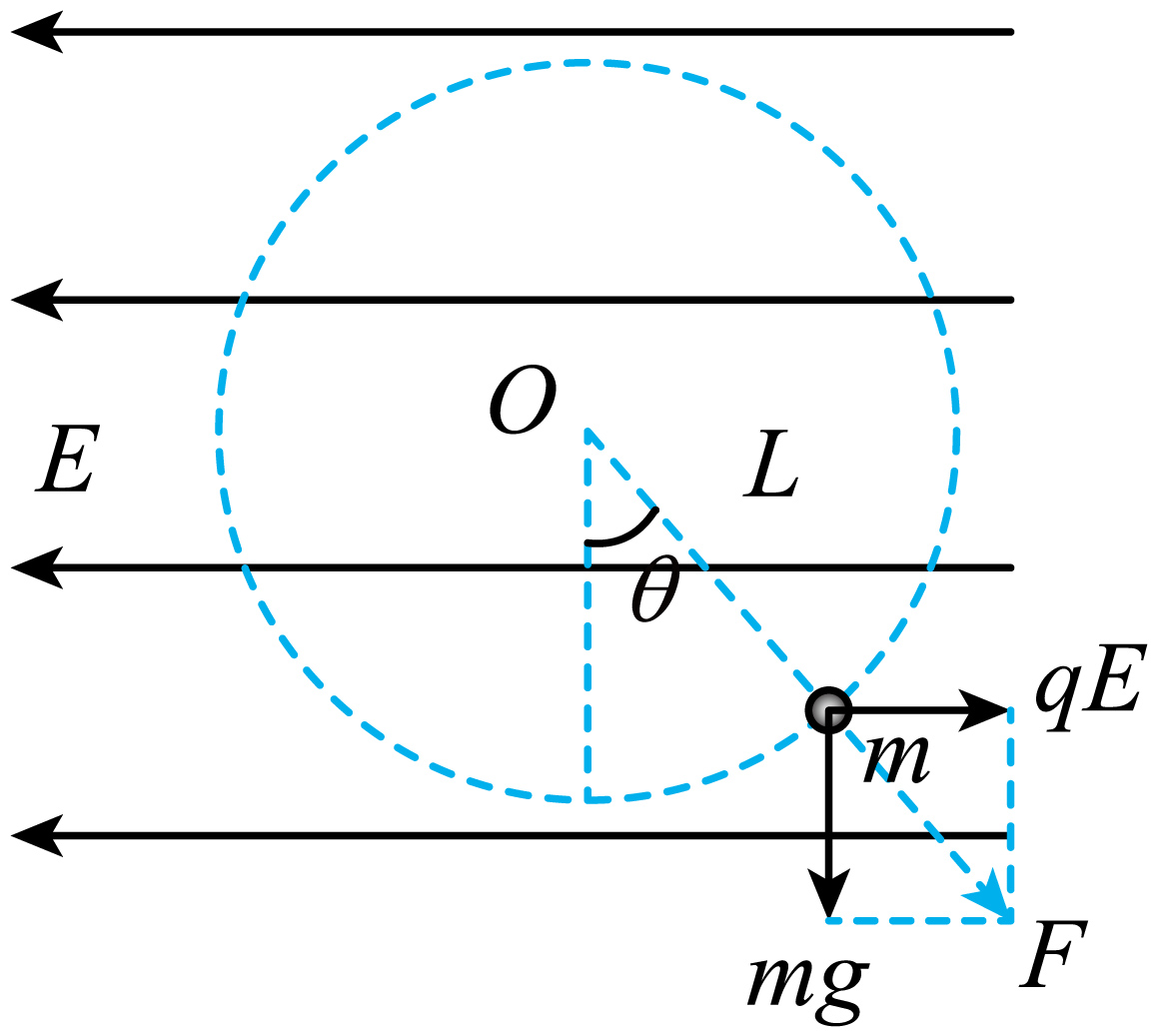
由平衡关系可知$\tan\theta=\dfrac{qE}{mg}$

解得$E=\dfrac{mg\tan\theta}{q}$

故$\rm A$正确；

$\rm B$．小球静止时细线与竖直方向成$\theta$角，则$A$点为小球绕$O$点在竖直平面内沿逆时针方向做圆周运动的等效最高点

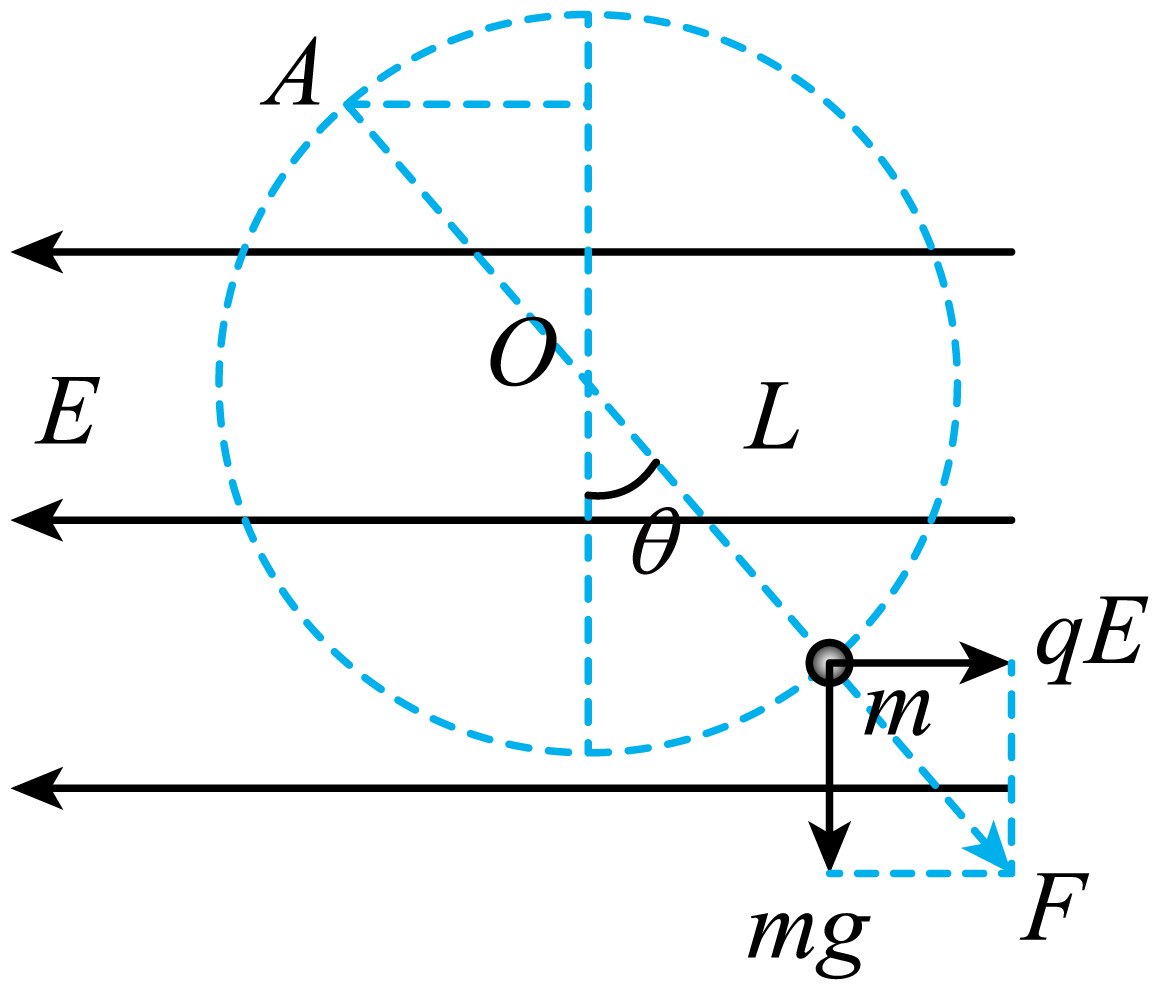
$A$点时小球的速度最小，动能最小，由牛顿第二定律可知$\dfrac{mg}{\cos\theta}=\dfrac{mv_{\min}^{2}}{L}$

动能$E_{\text{k}\min}=\dfrac{1}{2}mv_{\min}^{2}$

联立解得$E_{\text{k}\min}=\dfrac{mgL}{2\cos\theta}$

故$\rm B$错误；

$\rm C$．由机械能守恒定律可知，机械能的变化量等于除重力和弹簧弹力之外的其他力做的功，此处即电场力做的功。由题意可知，当小球运动到最左边与$O$点等高时，电场力做负功最多，机械能最小，故$\rm C$错误；

$\rm D$．小球从初始位置开始，在竖直平面内运动一周的过程中，电场力先做负功后做正功，所以电势能先增大后减小，故$\rm D$错误。

故选：$\rm A$。