| 匀变速直线运动的速度位移公式 题目答案及解析
稿件来源:高途
| 匀变速直线运动的速度位移公式题目答案及解析如下,仅供参考!
必修1
第二章 匀变速直线运动的研究
2.4 匀变速直线运动的速度与位移的关系
匀变速直线运动的速度位移公式
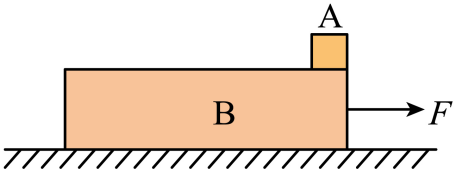
如图所示,现有一长方形物块$B$,其质量$M=20\;\rm kg$、长度$L=1\;\rm m$、高度为$h$、上表面光滑。物块$B$在水平拉力$F=80\;\rm N$的作用下在粗糙水平面上以$v_{0}=4\;\rm m/s$的速度匀速运动。现有一个小铁块$A$,质量为$m=10\;\rm kg$,将$A$无初速地放在$B$的最右端,同时撤去拉力$F$,求:(取$g=10\;\rm m/s^{2}$)
物块$B$与地面间的动摩擦因数;
$0.4$
"]]物块$B$做匀速运动时,对$B$受力分析,根据平衡条件有$F=f$
$F_{N}=Mg$
又$f=\mu F_{N}$
联立解得,物块$B$与地面间的动摩擦因数为$\mu =0.4$
铁块$A$放到$B$上时,物块$B$的加速度多大;
$6\\;\\rm m/s^{2}$
"]]铁块$A$放到$B$上时,对对$B$受力分析,根据牛顿第二定律有$\mu (m+M)g=Ma$
解得,物块$B$的加速度为$a=6\;\rm m/s^{2}$
讨论$h$取不同值时$A$落地瞬间与$B$左侧的水平距离。
见解析
"]]根据匀变速直线运动规律有$v^{2}-v_{0}^{2}=2(−a)L$
解得,$A$、$B$分离时,物块$B$的速度为$v=2\;\rm m/s$
$A$、$B$分离后,对$B$受力分析,根据牛顿第二定律有$\mu Mg=Ma_{2}$
解得,$A$、$B$分离后,物块$B$的加速度为$a_{2}=4\;\rm m/s^{2}$
则$A$、$B$分离后,物块$B$速度减为零的时间为$t_{0}=\dfrac{v}{a_{2}}=0.5\;\rm \text{s}$
$A$、$B$分离后,物块$B$滑行的距离为$x_{0}=\dfrac{1}{2}a_{2}t_{0}^{2}=0.5\;\rm \text{m}$
$A$、$B$分离后,$A$做自由落体运动,根据自由落体运动规律有$h=\dfrac{1}{2}gt^{2}$
可得,$A$下落的时间为$t=\sqrt{\dfrac{2h}{g}}$
当$A$落地时,$B$恰好停止,则$A$落地瞬间与$B$左侧的水平距离为$x_{0}$为$0.5\;\rm m$,此时$h=\dfrac{1}{2}gt_{0}^{2}=1.25\;\rm \text{m}$
则当$h\lt 1.25\;\rm m$时,$A$落地瞬间与$B$左侧的水平距离为$x=vt-\dfrac{1}{2}a_{2}t^{2}=2\left(\sqrt{\dfrac{h}{5}}-\dfrac{h}{5}\right)$
则当$h\geqslant 1.25\;\rm m$时,$A$落地瞬间与$B$左侧的水平距离为$0.5\;\rm m$。
| 匀变速直线运动的速度位移公式题目答案及解析(完整版)
