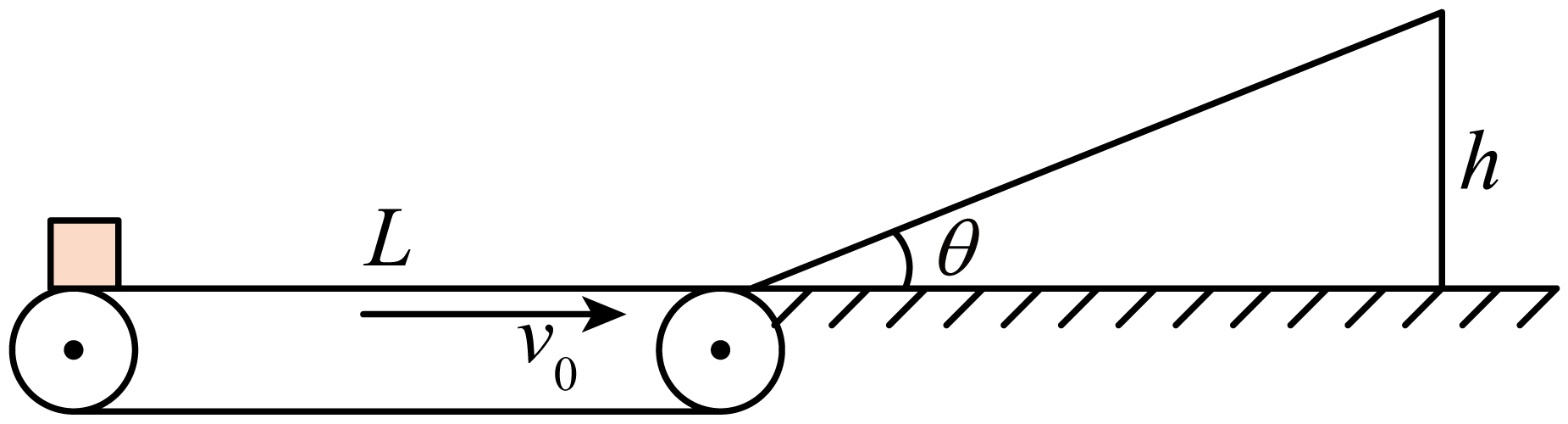
如图所示，水平传送带右端通过一段光滑的圆弧轨道与固定的斜面对接，传送带长$L=3\;\rm m$，沿顺时针方向以$v_{0}=5\;\rm m/s$的速度转动，斜面高$h=0.5\;\rm m$，倾角$\theta=30^\circ $，某时刻将一质量为$m=0.5\;\rm kg$的小物块无初速度轻放到传送带的左端，被传送带传送到右端经光滑的小圆弧运动到斜面上。物块与传送带和斜面之间的动摩擦因数分别为$\mu _{1}=0.5$、$\mu_{2}=\dfrac{\sqrt{3}}{3}$，不考虑物块的大小，忽略物块在小圆弧上运动的时间及速度大小的变化，物块运动到斜面上时在竖直平面内对物块施加力$F$，使物块沿斜面匀速上滑，已知$g=10\;\rm m/s^{2}$。以下说法正确的是$(\qquad)$

物块在传送带和斜面上运动的总时间为$1.3\\;\\rm s$

物块在传送带上运动过程中相对于传送带的路程为$2.5\\;\\rm m$

力$F$沿斜面向上时具有最小值，最小拉力$F$为$5\\;\\rm N$

力$F$斜向右上与斜面夹角为$30^\\circ$时拉力最小，最小拉力$F$为$\\dfrac{5\\sqrt{3}}{3}\\;\\rm {N}$

$\rm B$．物块在传送带上加速过程，由牛顿第二定律有$\mu _{1}mg=ma_{1}$

解得$a_{1}=5\;\rm m/s^{2}$

由运动学公式可得，物块运动的位移为$x_{1}=\dfrac{v_{0}^{2}}{2a_{1}}=\dfrac{5^{2}}{2 \times 5}{\;\rm m}=2.5{\;\rm m} \lt L=3\;\rm \text{m}$

物块运动的时间为$t_{1}=\dfrac{v_{0}}{a_{1}}=1\;\rm \text{s}$

之后物块随传送带一起匀速，则有$t_{2}=\dfrac{L-x_{1}}{v_{0}}=0.1\;\rm \text{s}$

物块相对于传送带运动过程，传送带的位移为$x_{2}=v_{0}t_{1}=5\;\rm m$

则物块相对于传送带运动路程为$s=x_{2} − x_{1}=2.5\;\rm m$，故$\rm B$正确；

$\rm A$．物块沿斜面匀速上滑，物块在斜面上运动的时间$t_{3}=\dfrac{\dfrac{h}{\sin 30{^\circ}}}{v_{0}}=0.2\;\rm \text{s}$

则物块在传送带和斜面上运动的总时间为$t=t_{1}+t_{2}+t_{3}=1.3\;\rm s$，故$\rm A$正确；

$\rm CD$．物块在斜面上运动过程中对物块受力分析，如图所示

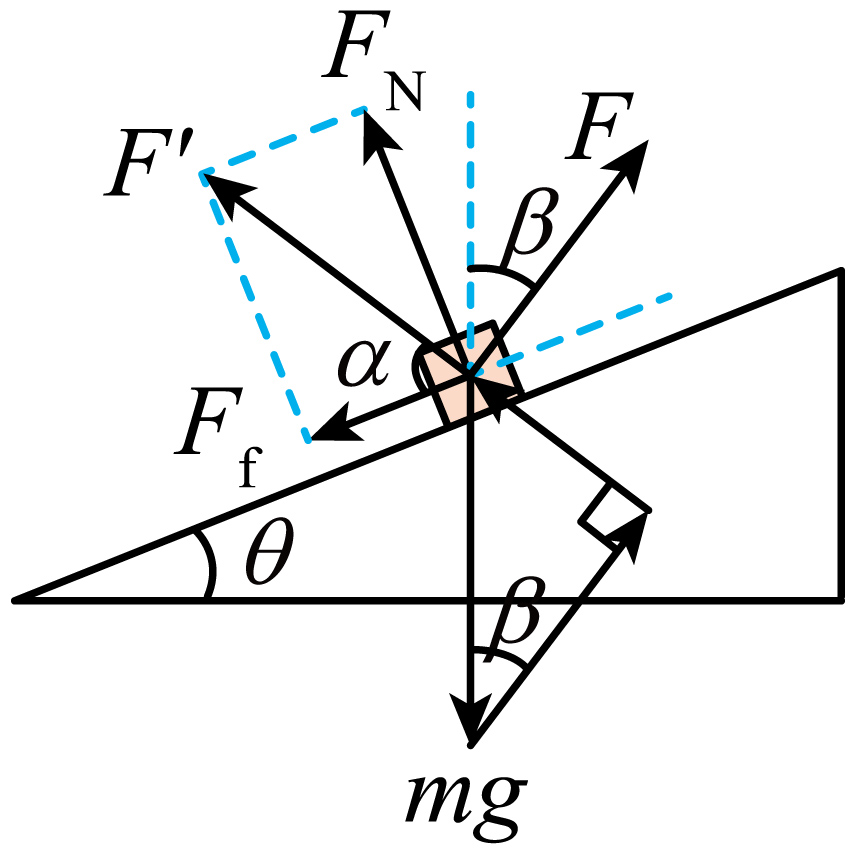
将斜面对物块的支持力$F_{N}$和摩擦力$F_{f}$等效成$F'$，则有$\tan\alpha=\dfrac{F_{N}}{F_{f}}=\dfrac{F_{N}}{\mu_{2}F_{N}}=\dfrac{3}{\mu_{2}}=\sqrt{3}$

解得$\alpha=60^\circ $，$F'$方向不变，然后将$mg$、$F$和拉力$F$矢量平移到一个三角形当中，当$F$与$F'$垂直时拉力$F$最小，则有$\beta=90^\circ − (180^\circ − 60^\circ − 60^\circ )=30^\circ $

$F_{\min}=mg\cos\beta=\dfrac{5\sqrt{3}}{2}{\;\rm N}$

则$F$与斜面的夹角$\gamma=60^\circ − \beta=30^\circ $，故$\rm CD$错误。

故选：$\rm AB$。