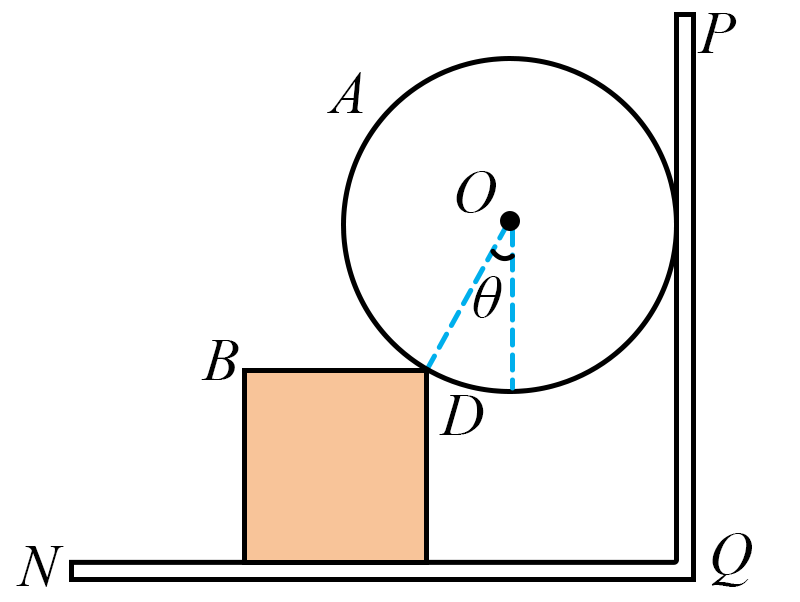
挡板$NQ$对物块$B$的支持力$F_{1}$，摩擦力$F_{f}$和$PQ$对球$A$的弹力$F_{2}$分别是多少？

$F_{1}=15\\;\\rm N$，$F_{f}=3.75\\;\\rm N$，$F_{2}=3.75\\;\\rm N$；

根据题意，对球$A$受力分析，如图所示

由平衡条件有

$F_{3}\sin \theta=F_{2}$，$F_{3}\cos \theta=mg$

解得$F_{2}=mg\tan \theta=3.75\;\rm N$，$F_{3}=\dfrac{mg}{\cos\theta}$

对球$A$和物块$B$整体受力分析，如图所示

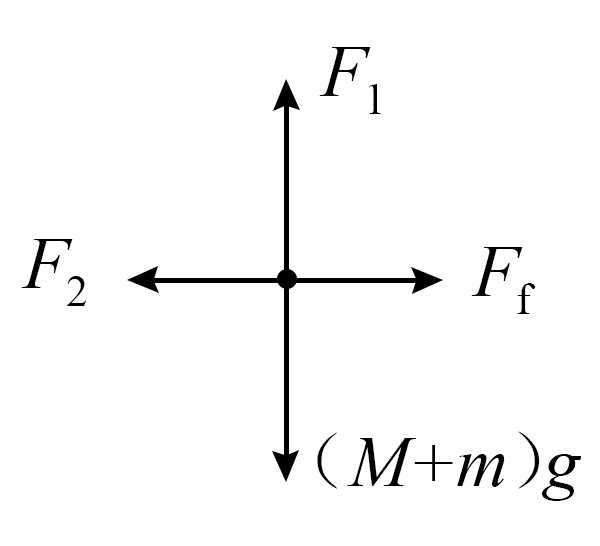
由平衡条件可得

$F_{1}=(M+m)g=15\;\rm N$，$F_{f}=F_{2}=3.75\;\rm N$；

若将物块$B$沿挡板$NQ$水平向左缓慢移动，移动过程中球$A$对挡板$PQ$和物块$B$的压力大小如何变化，为保持球$A$和物块$B$处于平衡状态，物块$B$向左移动的最大距离是多少？

球$A$对挡板$PQ$和物块$B$的压力均增大，$0.2\\;\\rm m$。

对$A$受力分析，如图所示

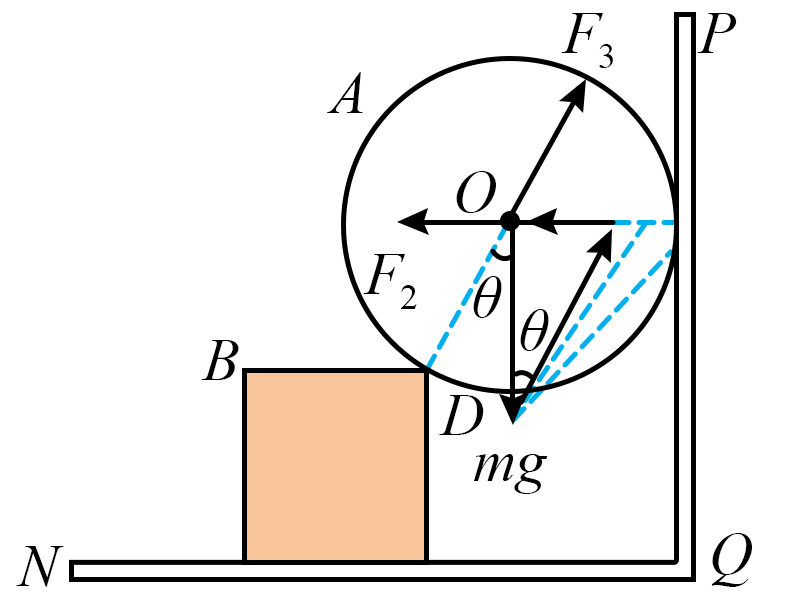
当物块$B$向左移动时$\theta$角增大，$F_{2}$和$F_{3}$增大，根据力作用的相互性知，球$A$对挡板$PQ$和物块$B$的压力均增大。初始状态物块$B$与挡板$PQ$的距离为$x_{1}=R+R\sin \theta$

解得$x_{1}=1.6\;\rm m$

临界时$F_{f\text{m}}=\mu(M+m)g=\dfrac{20}{3}{\;\rm N}$

$F_{2}=F_{f\text{m}}=\dfrac{20}{3}{\;\rm N}$

此时$\tan\theta'=\dfrac{F_{2}}{mg}=\dfrac{4}{3}$

即$\theta'=53^\circ $

物块与挡板$PQ$的距离$x_{2}=R+R\sin \theta'=1.8\;\rm m$

物块向左移动的最大距离$\Delta x=x_{2} − x_{1}=0.2\;\rm m$。