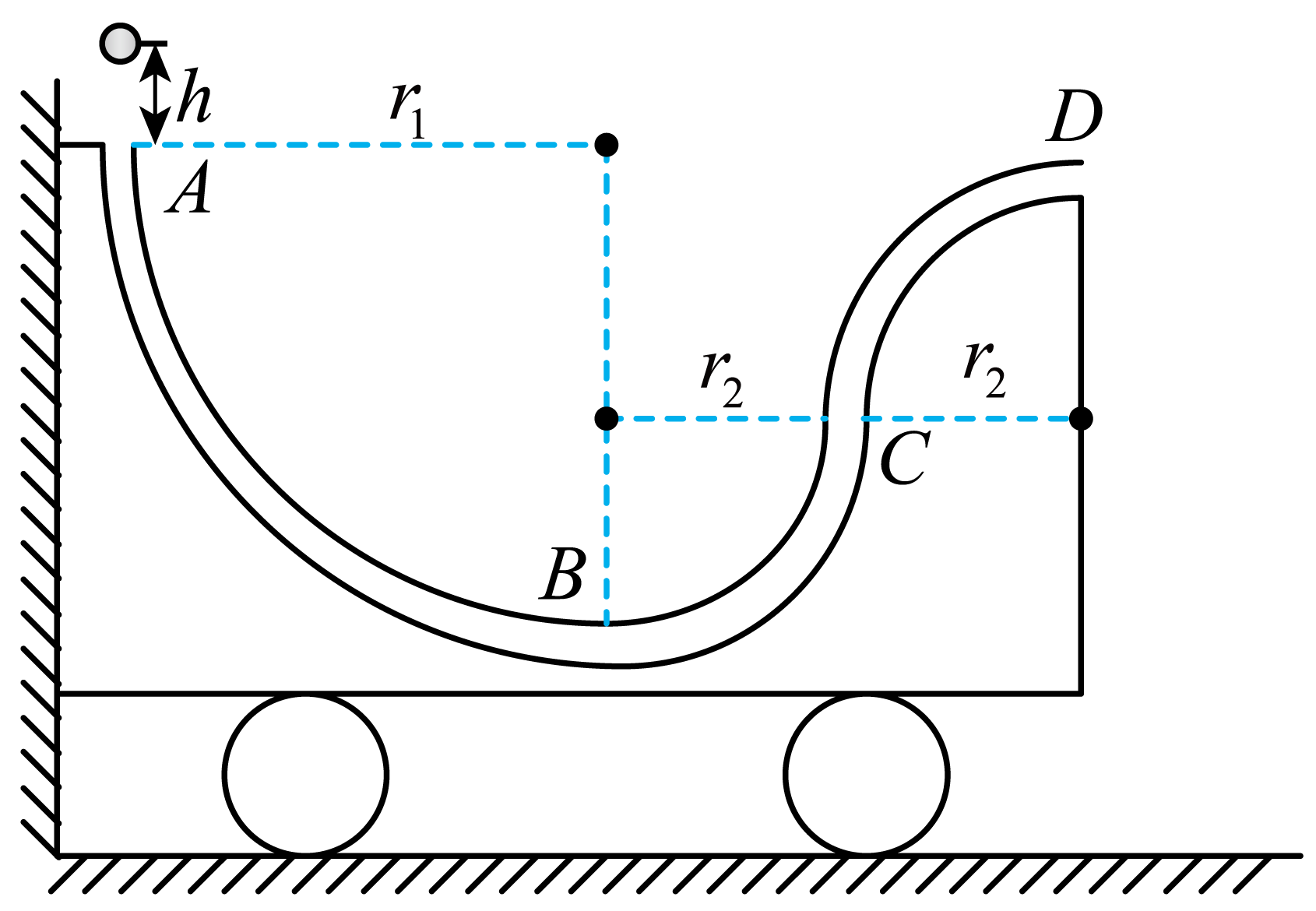
小球向右通过$B$点时的速度大小$v_{1}$；

$3\\;\\rm m/s$；

小球从静止释放运动至$B$点，根据动能定理得$mg\left( h+r_{1} \right)=\dfrac{1}{2}mv_{1}^{2}-0$

解得$v_{1}=3\;\rm m/s$

小球向上通过$C$点时，小车的速度大小$v_{2}$；

$1\\;\\rm m/s$；

小球运动至$C$点时，小球相对于小车竖直向上运动，水平方向上两者共速，根据水平方向动量守恒得$mv_{1}=(m+M)v_{2}$

解得$v_{2}=1\;\rm m/s$

小球能否从$D$点飞出？若能，请计算出飞出的速度大小；若不能，请说明理由。

不能，理由见解析

方法一：假设小球能够运动到$D$点时的速度为$v_{3}$，此时小车的速度为$v_{4}$，根据机械能守恒定律得$\dfrac{1}{2}mv_{1}^{2}=\dfrac{1}{2}mv_{3}^{2}+\dfrac{1}{2}Mv_{4}^{2}+mg \cdot 2r_{2}$

根据水平方向动量守恒得$mv_{1}=mv_{3}+Mv_{4}$

联立方程，代入数据计算发现：$v_{3}$和$v_{4}$无解，小球不能从$D$点飞出。

方法二：假设小球能够运动到的最大高度与$B$点的高度差为$H$，小球相对于小车的相对速度为零时达到最大高度，设此时速度为$v_{5}$，根据机械能守恒定律得$\dfrac{1}{2}mv_{1}^{2}=\dfrac{1}{2}(m+M)v_{5}^{2}+mgH$

根据水平方向动量守恒得$mv_{1}=(m+M)v_{5}$

联立方程，代入数据计算得$H=0.3{\;\rm m}\lt r_{1}=0.4\;\rm m$

小球不能从$D$点飞出。