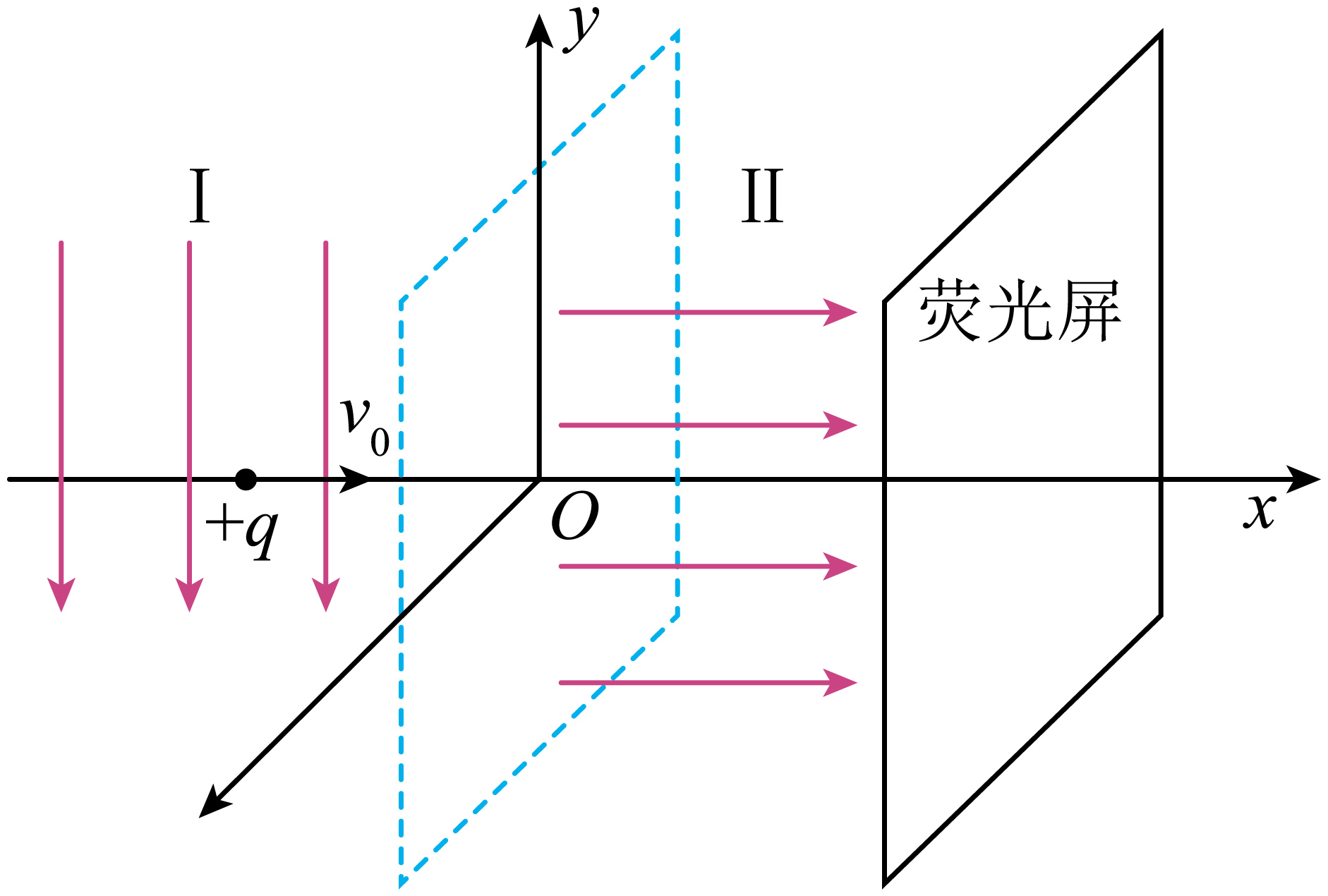
求粒子经过$yOz$平面时沿$y$轴的速度大小$v_{y}$。

$2v_{0}$

粒子在区域Ⅰ内，在$x$轴方向做匀速直线运动，可得粒子在区域Ⅰ内的时间为$t_{1}=\dfrac{L}{v_{0}}$

因受到电场力的作用，粒子在区域Ⅰ内时，在$y$轴上做匀加速运动

可得$L=\dfrac{1}{2}a_{1}t_{1}^{2}$

解得$a_{1}=\dfrac{2v_{0}^{2}}{L}$

则可得粒子经过$yOz$平面时沿$y$轴的速度大小$v_{y}=a_{1}t_{1}=2v_{0}$

若荧光屏与$x$轴交点的$x$轴坐标为$\dfrac{3\pi mv_{0}}{qB}$，求粒子在磁场中的运动时间$t$。

$\\dfrac{3\\pi m}{qB}$

因在区域Ⅱ内的磁场方向沿$x$轴正方向，则将粒子进入区域Ⅱ内的速度分解为沿$x$轴方向和垂直于$x$轴方向，沿$x$轴方向的速度大小为$v_{0}$，垂直于$x$轴方向的速度大小为$2v_{0}$，沿$y$轴负方向，则可得粒子在磁场中的运动时间为$t=\dfrac{\dfrac{3\pi mv_{0}}{qB}}{v_{0}}=\dfrac{3\pi m}{qB}$

若粒子击中荧光屏时$z$轴坐标为$\dfrac{mv_{0}}{qB}$，求荧光屏与$x$轴交点的$x$坐标。

$\\left( n+\\dfrac{1}{6} \\right)\\dfrac{2\\pi mv_{0}}{Bq}(n=0,1,2,3,\\cdots)$或$\\left( n-\\dfrac{1}{6} \\right)\\dfrac{2\\pi mv_{0}}{Bq}(n=1,2,3,\\cdots)$

根据洛伦兹力提供向心力，可得$m\dfrac{(2v_{0})^{2}}{R}=Bq·2v_{0}$

解得$R=\dfrac{2mv_{0}}{Bq}$

已知粒子击中荧光屏时$z$轴坐标为$\dfrac{mv_{0}}{qB}$，即在$z$轴方向上的位移为$d=\dfrac{mv_{0}}{Bq}$

设粒子在$yOz$平面上的速度偏转的角度为$\theta$，则可得$\cos\theta=\dfrac{R-d}{R}=\dfrac{1}{2}$

解得$\theta=2n\pi+\dfrac{\pi}{3}(n=0,1,2,3,\cdots)$

或$\theta=2n\pi-\dfrac{\pi}{3}(n=1,2,3,\cdots)$

可知粒子在磁场中运动的周期为$T=\dfrac{2\pi m}{qB}$

则粒子在磁场中经历的时间为$t=\dfrac{\theta}{2\pi}T=\left( n+\dfrac{1}{6} \right)\dfrac{2\pi m}{Bq}(n=0,1,2,3,\cdots)$

或$t=\left( n-\dfrac{1}{6} \right)\dfrac{2\pi m}{Bq}(n=1,2,3,\cdots)$

荧光屏与$x$轴交点的$x$坐标为$x=v_{0}t=\left( n+\dfrac{1}{6} \right)\dfrac{2\pi mv_{0}}{Bq}(n=0,1,2,3,\cdots)$

或$x=\left( n-\dfrac{1}{6} \right)\dfrac{2\pi mv_{0}}{Bq}(n=1,2,3,\cdots)$