| 匀变速直线运动的速度位移公式 题目答案及解析
稿件来源:高途
| 匀变速直线运动的速度位移公式题目答案及解析如下,仅供参考!
必修1
第二章 匀变速直线运动的研究
2.4 匀变速直线运动的速度与位移的关系
匀变速直线运动的速度位移公式
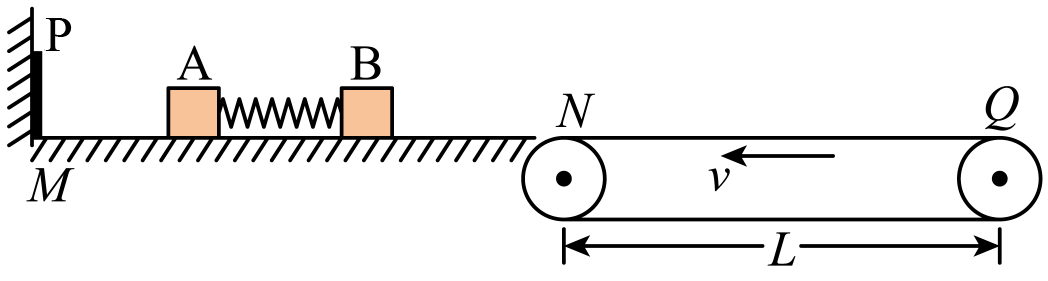
如图所示,光滑水平面$MN$的左端有一弹性挡板$P$(碰撞时无能量损失),右端$N$与处于同一高度的水平传送带之间的距离可忽略,传送带水平部分$NQ$的长度$L=4\;\rm m$,传送带逆时针匀速转动,其速度$v=2\;\rm m/s$。$MN$上放置着两个可视为质点的质量为$m_{A}=4\;\rm kg$、$m_{B}=1\;\rm kg$的小物块$A$、$B$,开始时$A$、$B$都静止,$A$、$B$间压缩一锁定的轻质弹簧,其弹性势能$E_{P}=10\;\rm J$。现解除锁定,弹簧弹开$A$、$B$后迅速移走弹簧,$g=10\;\rm m/s^{2}$。求:
物块$A$、$B$被弹开时各自的速度大小;
$v_{A}=1\\;\\rm m/s$,$v_{B}=4\\;\\rm m/s$;
"]]$A$、$B$物块被弹簧弹开的过程中,由动量守恒定律得$m_{A}v_{A}-m_{B}v_{B}=0$
由能量守恒定律得$E_{\text{p}}=\dfrac{1}{2}m_{A}v_{A}^{2}+\dfrac{1}{2}m_{B}v_{B}^{2}$
联立解得$v_{A}=1\;\rm m/s$
$v_{B}=4\;\rm m/s$
已知两物块将在水平面$MN$上发生碰撞,则小物块$B$与传送带间的动摩擦因数至少为多大;
$0.2$;
"]]要使两物块能在水平面$MN$上发生碰撞,小物块$B$不能在传送带的$Q$端掉下,则小物块$B$在传送带上最多减速运动到$Q$端速度减为零,设减速过程加速度大小至少为$a$,动摩擦因数至少为$\mu $,有$\mu m_{B}g=m_{B}a$
$v_{B}^{2}=2aL$
联立解得$\mu =0.2$
即小物块$B$与传送带间的动摩擦因数至少为$0.2$。
若物块$A$、$B$与传送带间的动摩擦因数都等于第($2$)问中的临界值,且两物块在水平面$MN$上碰撞后结合成整体。在此后两物块整体第一次滑上传送带到第一次减速至零的过程中,两物块整体与传送带间产生的总热量。
$4.4\\;\\rm J$或$15.6\\;\\rm J$
"]]因为物块$B$第一次冲上传送带的速度$v_{B}=4\;\rm m/s$大于传送带速度$v=2\;\rm m/s$,所以物块$B$返回过程先加速后匀速,到达水平面$MN$上时的速度等于传送带速度,故$v'_{B}=v=2\;\rm m/s$
①若两物块$A$、$B$在水平面$MN$上相向碰撞结合成整体,设共同速度为$v_{1}$,根据动量守恒定律,可得 $m_{A}v_{A}-m_{B}v'_{B}=(m_{A}+m_{B})v_{1}$
解得$v_{1}=0.4\;\rm m/s$
方向向右
两物块整体第一次滑上传送带到第一次减速至零的过程用时$t_{1}=\dfrac{v_{1}}{a}$
两物块整体相对传送带运动的距离为$\Delta x_{1}=vt_{1}+\dfrac{1}{2}v_{1}t_{1}$
解得$\Delta x_{1}=0.44\;\rm m$
故两物块整体第一次滑上传送带到第一次减速至零的过程中,两物块与传送带间产生的总热量为$Q_{1}=\mu (m_{A}+m_{B})g ⋅ \Delta x_{1}$
解得$Q_{1}=4.4\;\rm J$
②若两物块$A$、$B$在水平面$MN$上同向碰撞结合成整体,设共同速度为$v_{2}$,根据动量守恒有$m_{A}v_{A}+m_{B}v'_{B}=(m_{A}+m_{B})v_{2}$
解得$v_{2}=1.2\;\rm m/s$
方向向左。
两物块整体与弹性挡板$P$碰撞无能量损失,碰后速度大小仍为$v_{2}=1.2\;\rm m/s$,方向向右。
两物块整体第一次滑上传送带到第一次减速至零的过程用时$t_{2}=\dfrac{v_{2}}{a}$
两物块整体相对传送带运动的距离为$\Delta x_{2}=vt_{2}+\dfrac{1}{2}v_{2}t_{2}$
解得$\Delta x_{2}=1.56\;\rm m$
故两物块整体第一次滑上传送带到第一次减速至零的过程中,两物块与传送带间产生的总热量为$Q_{2}=\mu (m_{A}+m_{B})g ⋅ \Delta x_{2}$
解得$Q_{2}=15.6\;\rm J$
即两物块整体与传送带间产生的总热量是$4.4\;\rm J$或$15.6\;\rm J$。
| 匀变速直线运动的速度位移公式题目答案及解析(完整版)
