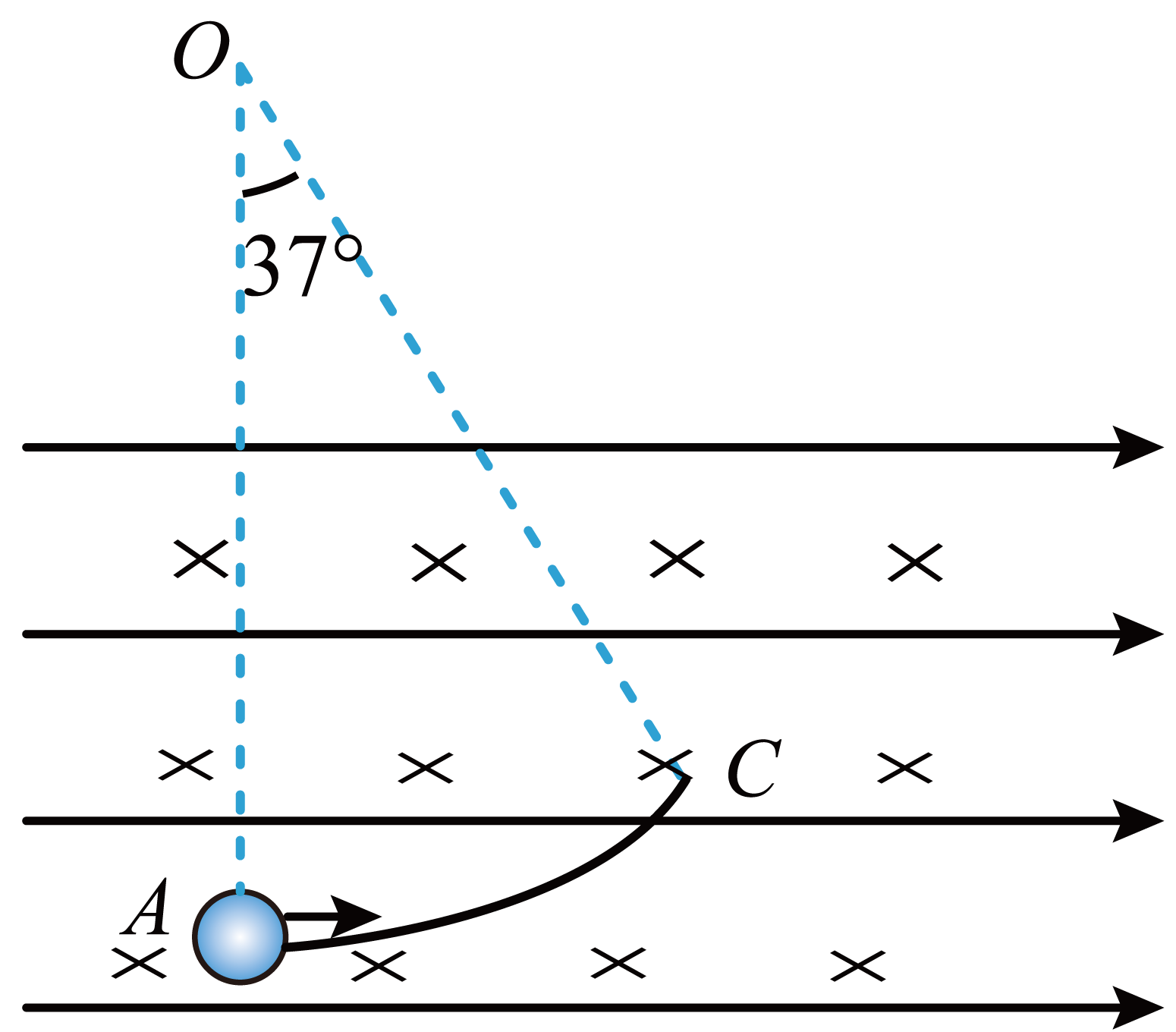
匀强电场的场强$E$；

$E=6\\;\\rm N/C$；

当小球离开圆弧轨道后，对其受力分析如图所示

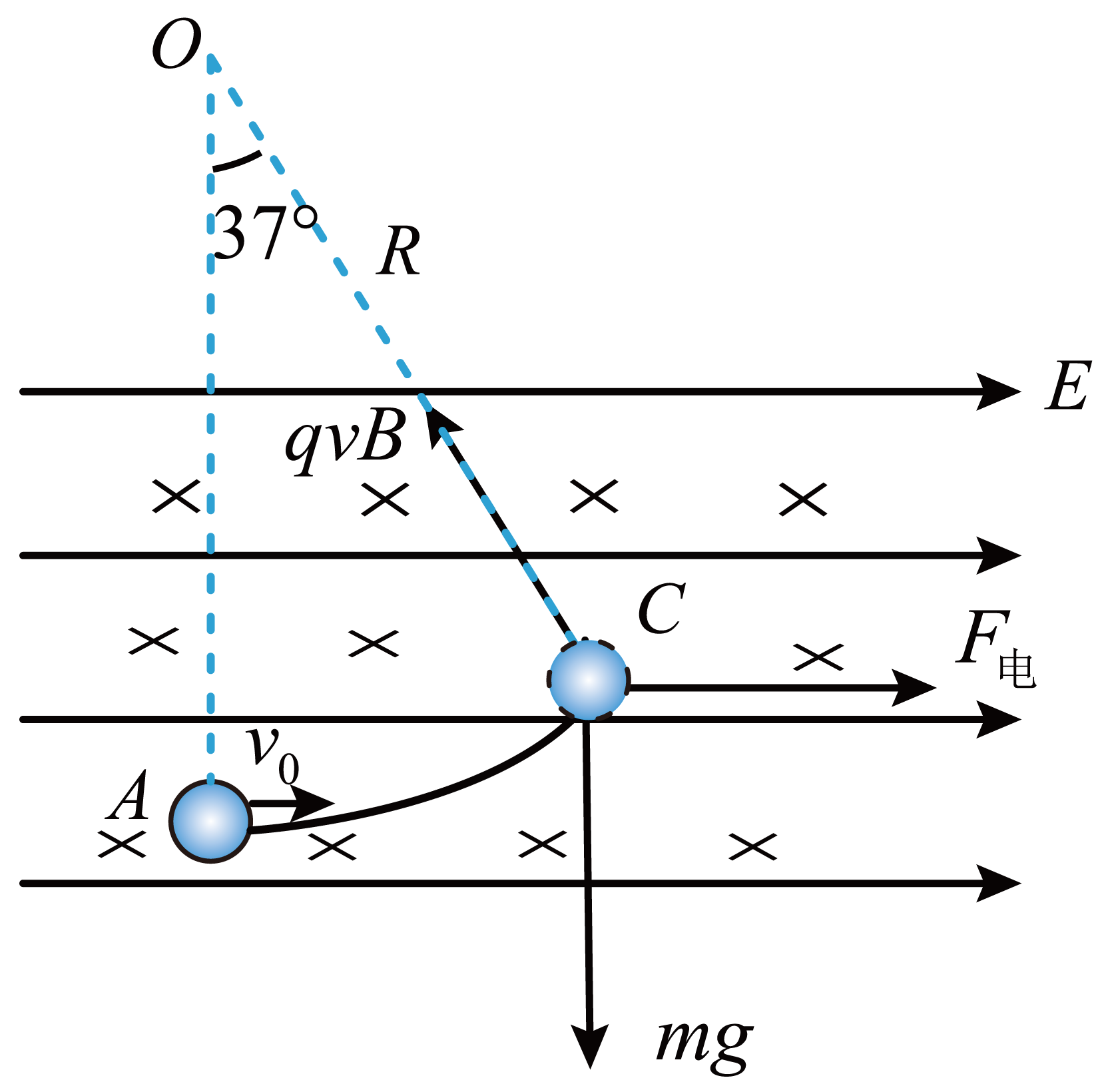
由平衡条件得$F_{电}=qE=mg\tan\theta$

代入数据解得$E=6\;\rm N/C$；

小球经过$C$点时的速率；

$v_{C}=4\\;\\rm m/s$；

小球从进入圆弧轨道到离开圆弧轨道的过程中，由动能定理得$qER\sin\theta-mgR\left( 1-\cos\theta \right)=\dfrac{1}{2}mv_{C}^{2}-\dfrac{1}{2}mv_{A}^{2}$

代入数据得$v_{C}=4\;\rm m/s$；

小球射入至圆弧轨道$A$端的瞬间，小球对轨道的压力（计算结果保留两位有效数字）。

$F_{N} ≈ 2.5 \\times 10^{-3}\\;\\rm N$，竖直向下。

根据小球经过$C$点时的受力分析图可知$F_{磁}=qv_{C}B=\dfrac{mg}{\cos\theta}$

解得$B=2.5\;\rm T$

分析小球经过$A$处时，由向心力公式可知$F_{{N}}+qv_{A}B-mg=m\dfrac{v_{A}^{2}}{R}$

代入数据得$F_{N} ≈ 2.5 \times 10^{-3}\;\rm N$

由牛顿第三定律得，小球对轨道的压力为$F_{N} ≈ 2.5 \times 10^{-3}\;\rm N$

方向竖直向下。