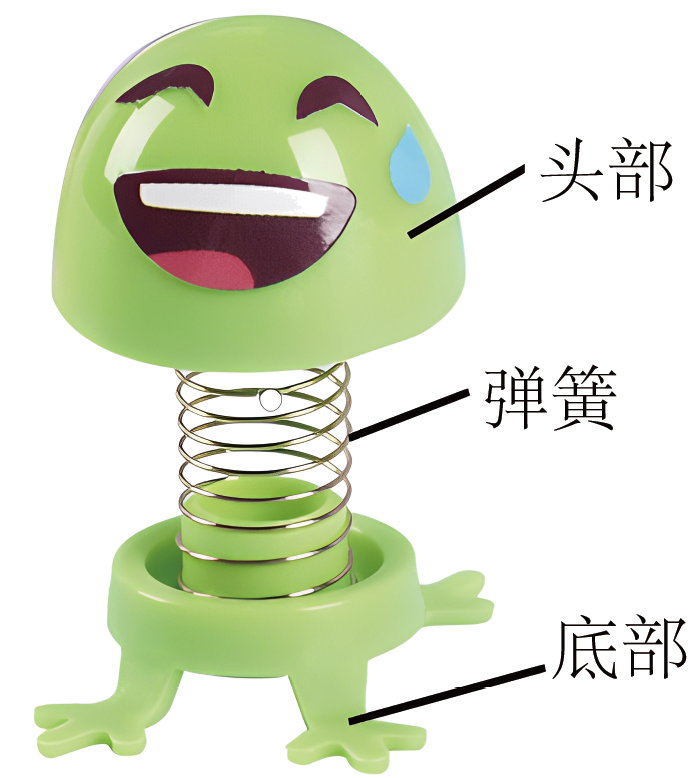
如图所示为一款近期火爆的玩具“弹簧小人”，由头部、轻质弹簧及底部组成，头部质量为$m$，底部质量为$\dfrac{m}{2}$，弹簧劲度系数为$k$。将“弹簧小人”置于水平桌面上，轻压头部后由静止释放，头部会不停地上下振动，不计摩擦和空气阻力，重力加速度为$g$，弹簧始终处于弹性限度内。下列判断正确的是$(\qquad)$

若头部刚释放时的加速度大小为$g$，则振动过程中底部能离开桌面

若头部刚释放时的加速度大小为$g$，则振动过程中“弹簧小人”对桌面的最大压力为$3mg$

若振动过程中底部恰好能离开桌面，头部在最高点时的加速度为$\\dfrac{3}{2}g$

若振动过程中底部恰好能离开桌面，则释放头部时弹簧压缩量为$\\dfrac{2mg}{k}$

$\rm A$．设头部在初始位置时弹簧的压缩量为$x_{0}$，对头部列平衡方程$mg=kx_{0}$

施加力$F$后弹簧再压缩$x$，头部的平衡方程为$F+mg=k(x_{0}+x)$

若刚释放时头部的加速度大小为$g$，根据牛顿第二定律得$k(x_{0}+x)-mg=mg$

则$F=mg$

解得$kx=mg$

撤去力$F$的瞬间，头部所受的回复力$F_{回}=k(x_{0}+x)-mg=kx$

当头部向上运动到初始位置上方距离也是$x$时，由对称性知$F_{回}=kx$，而$kx=mg$，可见头部所受弹簧弹力恰好是零，以底部为研究对象，受力分析知地面对底部的支持力为$N=\dfrac{m}{2}g$

因此小人在振动过程中底部不能离开桌面，故$\rm A$错误；

$\rm B$．初始状态时，对桌面的压力最大，此时对“弹簧小人”受力分析$F+\left(m+\dfrac{m}{2}\right)g=N$

解得$N=2.5mg$

根据牛顿第三定律，桌面对“弹簧小人”的支持力等于“弹簧小人”对桌面的压力，故$\rm B$错误；

$\rm C$．若小人在振动过程中底部恰好能离开桌面，即当头部在最高点时，底部受到桌面的弹力为$0$，受力分析得弹簧此时的弹力等于底部的重力$kx_{2}=\dfrac{1}{2}mg$

此时对头部受力分析，根据牛顿第二定律有$mg+\dfrac{1}{2}kx_{2}=ma$

故头部在最高点的加速度为$\dfrac{3}{2}g$，故$\rm C$正确；

$\rm D$．若小人在振动过程中底部恰好不能离开桌面，开始施加力$F'$后弹簧再压缩$x'$，头部的平衡方程为$F'+mg=k(x_{0}+x')$

分析得$kx'=mg+\dfrac{1}{2}mg=\dfrac{3}{2}mg$

则轻压头部释放时弹簧的压缩量为$\Delta x=x_{0}+x'=\dfrac{5mg}{2k}$

故$\rm D$错误。

故选：$\rm C$。