| 振动图像和波动图像综合 题目答案及解析
稿件来源:高途
| 振动图像和波动图像综合题目答案及解析如下,仅供参考!
选修3-4
第十二章 机械波
12.2 波的图像
振动图像和波动图像综合
图甲中,青蛙在平静的水面上鸣叫时引起水面振动。把水波视作横波,以青蛙所在位置为原点$O$,某时刻波源垂直$xoy$平面振动所产生波的示意图如图乙所示,实线圆、虚线圆分别表示相邻的波峰和波谷,图丙为某质点的振动图像,求:
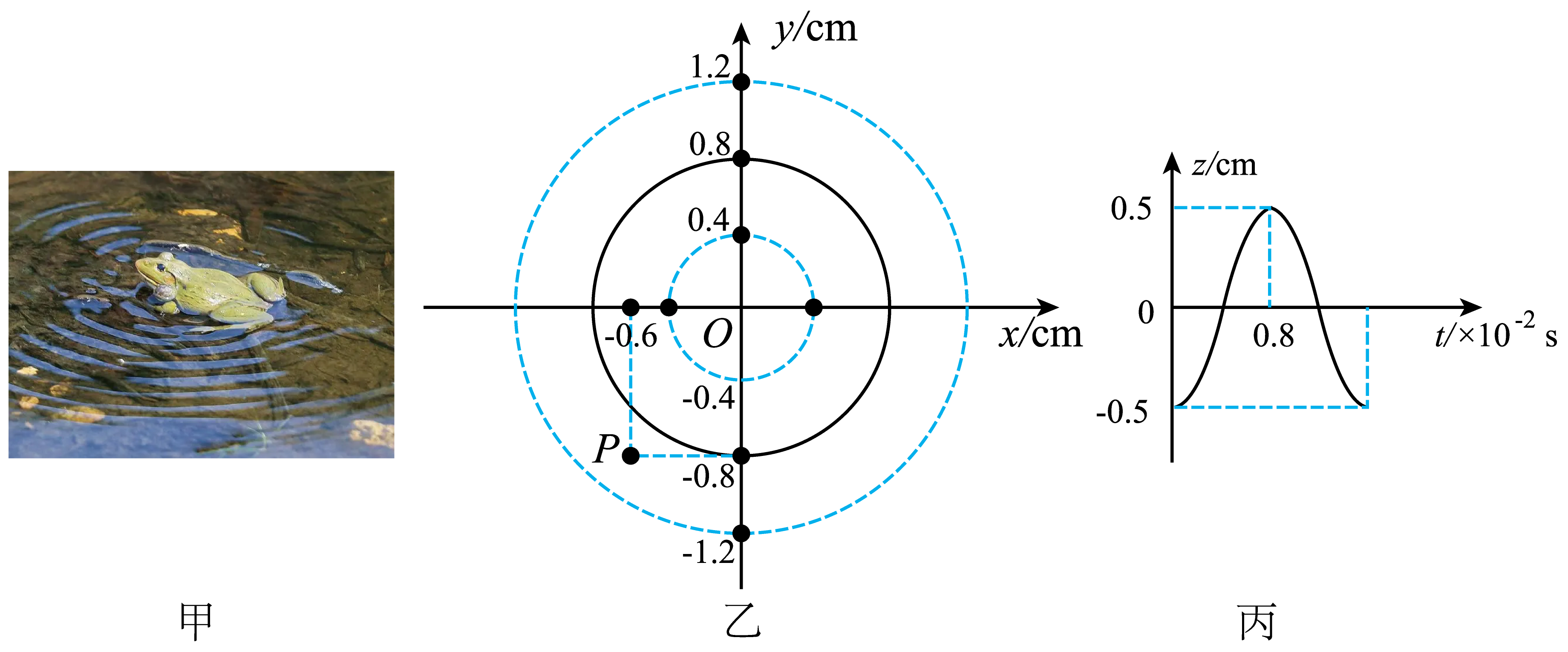
波在水中的传播速度大小$v$;
$0.5\\;\\rm m/s$;
"]]实线圆、虚线圆分别表示$t=0$时刻相邻的波峰和波谷,由图乙可知$\dfrac{\lambda}{2}=0.4\;\rm \text{cm}$
由图乙可知周期$T=0.016\;\rm s$
则波在水中的传播速度大小为$v=\dfrac{\lambda}{T}=0.5\;\rm \text{m/s}$
从图乙所示状态开始,$P$点到达波谷所需时间$\Delta t$。
$\\Delta t=(1.6n+1.2)\\times 10^{-2}\\;{\\rm s}(n=0,1,2 ⋅ ⋅⋅)$
"]]根据题意可知$P$处此时处平衡位置,从图乙所示状态开始,$P$点第$1$次到达波谷所需时间为$t_{1}=\dfrac{S_{OP}-\dfrac{\lambda}{2}}{v}$
代入数据解得$t_{1}=1.2 \times 10^{-2}\;\rm s$
则$P$点到达波谷的所有时间为$\Delta t=t_{1}+nT(n=1,2,3…)$
代入数据解得$\Delta t=(1.6n+1.2)\times 10^{-2}\;{\rm s}(n=0,1,2 ⋅ ⋅⋅)$
| 振动图像和波动图像综合题目答案及解析(完整版)
