| 动量守恒之木板滑块模型 题目答案及解析
稿件来源:高途
| 动量守恒之木板滑块模型题目答案及解析如下,仅供参考!
选修3-5
第十六章 动量守恒定律
16.3 动量守恒定律
动量守恒之木板滑块模型
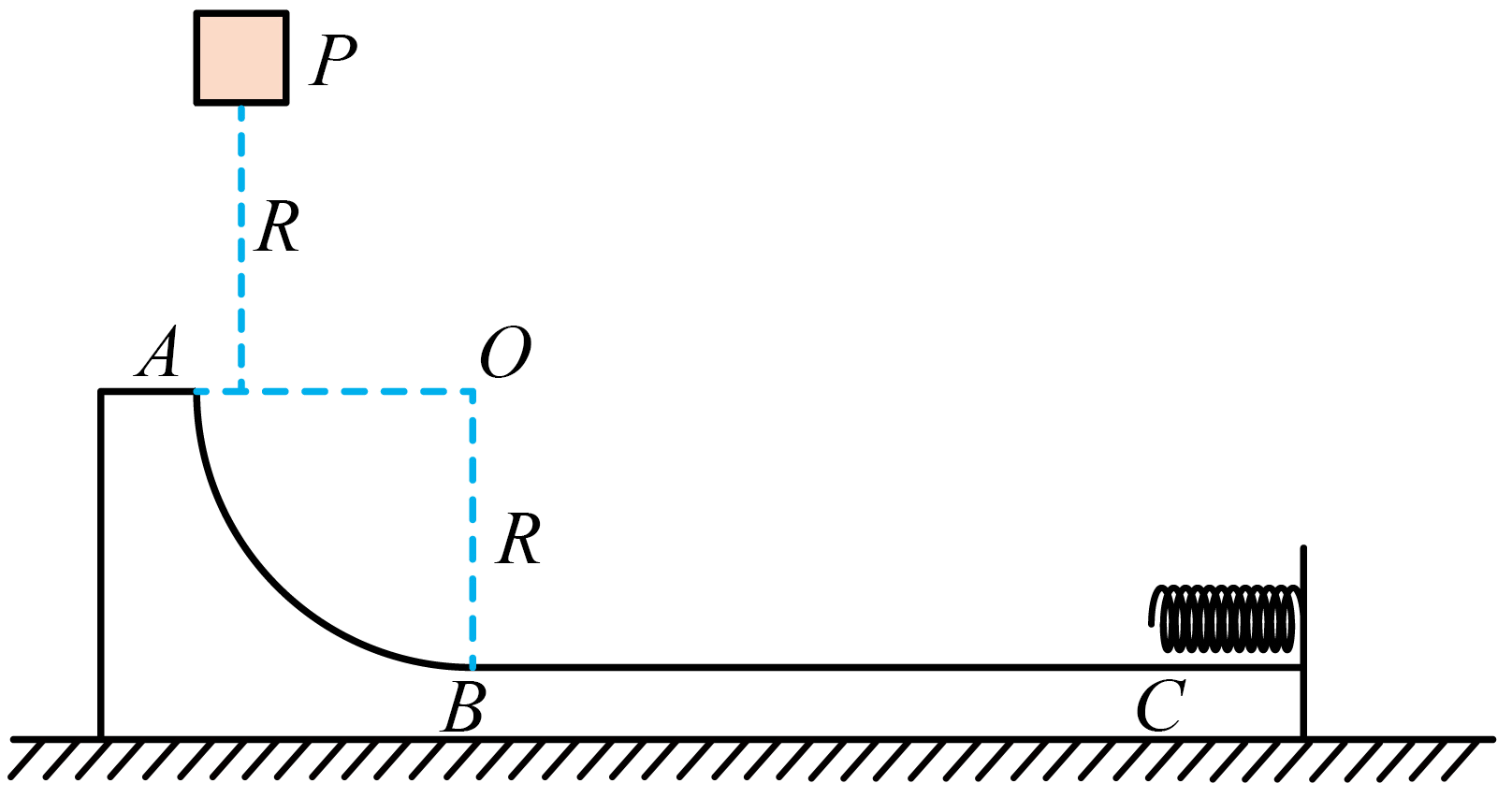
如图所示,左端为四分之一圆弧的木板静止置于光滑水平面上,圆弧与木板水平部分相切于$B$点。在木板右端固定一轻弹簧,其自由端位于木板上$C$点正上方,将质量为$m$的小物块$P$(可视为质点)自$A$点上方高度为$R$处的某点静止释放,沿切线进入圆弧,已知长木板质量为$5m$,圆弧的半径为$R$,$ BC=2R$,$BC$段粗糙,与小物块间的动摩擦因数为$\mu $,其余部分均光滑。重力加速度为$g$。
若将木板锁定在水平面上,求小物块到达圆弧最低点时受到木板的支持力大小$F_{\rm N}$;
$5mg$;
"]]当木板固定在水平面上时,则根据动能定理$mg \times 2R=\dfrac{1}{2}mv_{0}^{2}$
物块在最低点时,所受支持力和重力的合力提供向心力$F_{\text{N}}-mg=m\dfrac{v_{0}^{2}}{R}$
解得$F_{\rm N}=5mg$
若木板未锁定,求小物块到达圆弧最低点时,小物块速度大小$v_{1}$与木板速度大小$v_{2}$;
$v_{2}=\\sqrt{\\dfrac{2gR}{15}}$, $v_{1}= 5\\sqrt{\\dfrac{2gR}{15}}$,;
"]]若木板未锁定,则木板在水平方向上动量守恒,物块在圆弧上运动时系统机械能守恒$mv_{1}=5mv_{2}$
$mg \times 2R=\dfrac{1}{2}mv_{1}^{2}+\dfrac{1}{2} \times 5mv_{2}^{2}$
解得$v_{1}=5\sqrt{\dfrac{2gR}{15}}$,$v_{2}=\sqrt{\dfrac{2gR}{15}}$
求在($2$)问情况中弹簧弹性势能的最大值$E_{pm}$。
$2mgR(1-\\mu )$
"]]木板和物块动量守恒,当木板和物块共速时,弹簧弹性势能的最大,取向左为正方向$5mv_{2} − mv_{1}=6mv$
根据能量守恒$mg \times 2R=\mu mg \times 2R+\dfrac{1}{2} \times 6mv^{2}+E_{\text{p}}$
解得$E_{\rm p}=2mgR(1-\mu )$
| 动量守恒之木板滑块模型题目答案及解析(完整版)
