高中 | 示波管 题目答案及解析
稿件来源:高途
高中 | 示波管题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
示波管
如图所示的示波管模型中,电荷量为$e$、质量为$m$的电子从灯丝$K$发出,经加速电场加速后,从中心孔$S$沿极板中心线$SO$以速度$v$水平射入平行板电容器,穿出偏转电场后,又经过一段匀速直线运动,最后打到荧光屏上的$C$点。已知平行板电容器两极板间的电压为$U$,板长为$L$,两极板间的距离为$d$,偏转电场两极板右端到荧光屏的距离为$L$,不计电子重力。
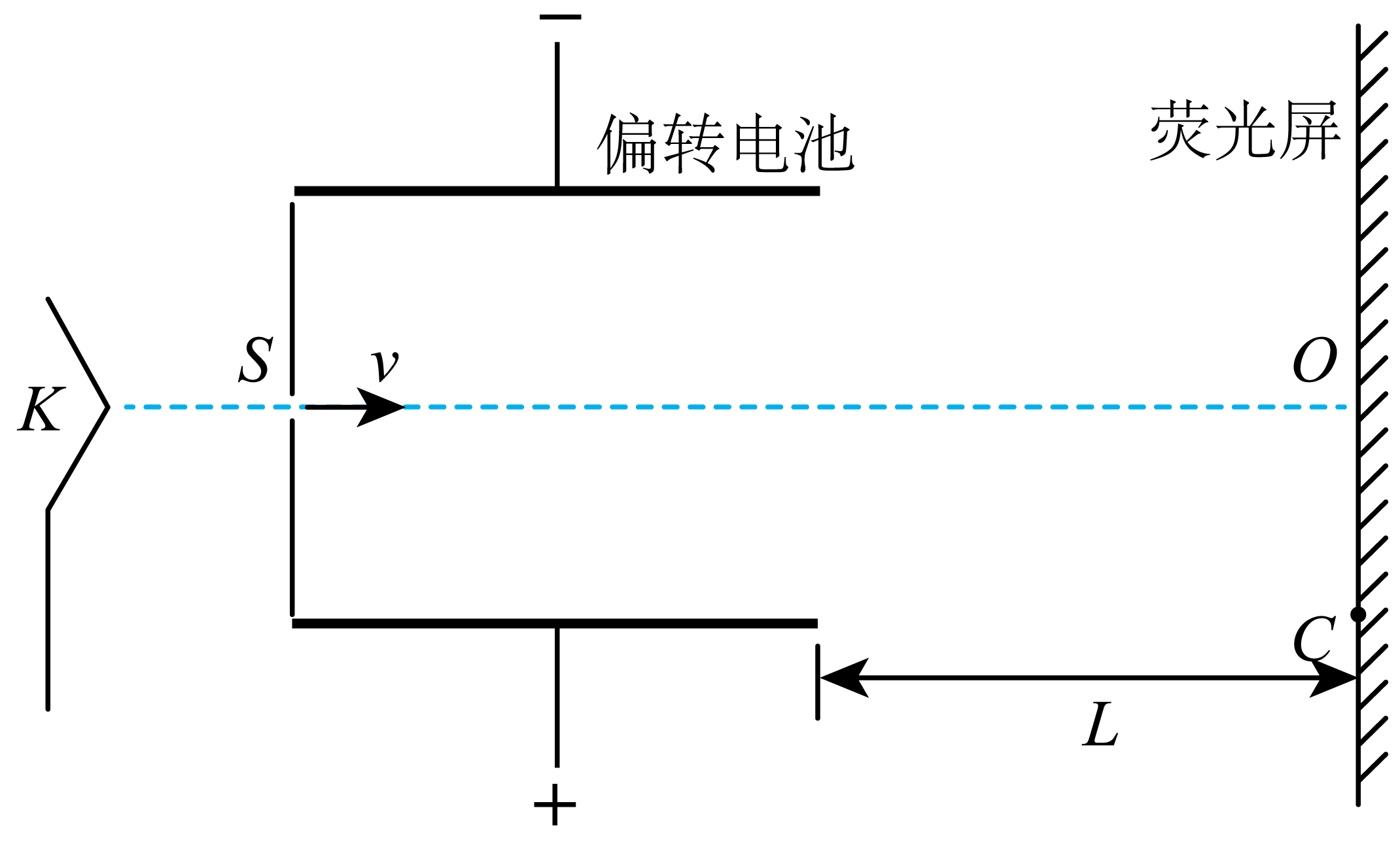
求荧光屏上$O$、$C$两点间的距离;
$OC= \\dfrac{3eUL^{2}}{2mdv^{2}}$
"]]粒子在偏转电场中做类平抛运动,如图所示:
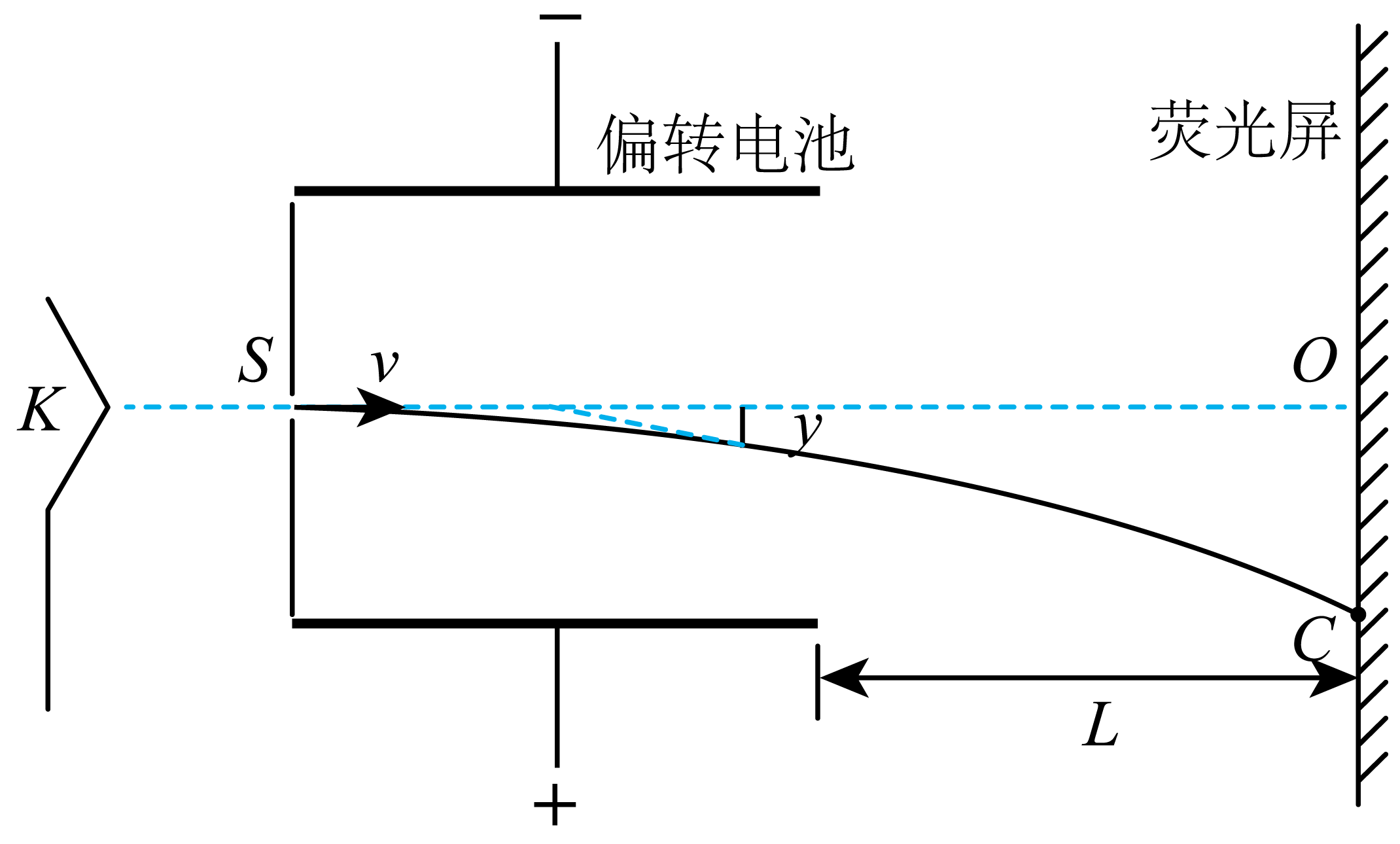
垂直电场方向有$L=vt$
沿电场方向$e\dfrac{U}{d}=ma$
侧移量$y=\dfrac{1}{2}at^{2}$
解得$y=\dfrac{eUL^{2}}{2mdv^{2}}$
由几何关系可知$\dfrac{y}{OC}=\dfrac{\dfrac{1}{2}L}{L+\dfrac{1}{2}L}$
得荧光屏上间的距离$OC=\dfrac{3eUL^{2}}{2mdv^{2}}$
将平行板电容器与电源断开,仅增大两极板间距,发现电子仍打到若光屏上的$C$点,请列式说明原因。
答案见解析
"]]因电容器与电源断开,两板上所带电量不变,根据$E=\dfrac{U}{d}$,$U=\dfrac{Q}{C}$,$C=\dfrac{\varepsilon_{{r}}S}{4\pi kd}$
解得$E=\dfrac{4\pi kQ}{\varepsilon_{{r}}S}$
仅增大两极板间距,板间电场强度不变,带电粒子在电场中的受力情况不变,则运动情况不变,故该电子仍能打到若光屏上而显示亮点$C$。
高中 | 示波管题目答案及解析(完整版)
