高中 | 洛伦兹力 题目答案及解析
稿件来源:高途
高中 | 洛伦兹力题目答案及解析如下,仅供参考!
选修3-1
第三章 磁场
3.5 运动电荷在磁场中受到的力
洛伦兹力
如图所示是质谱仪的结构简化图。在速度选择器上方存在有界磁场区域,该区域上边界为直线,下边界由直线$MN$、半圆$NP$、直线$PQ$组成,$M$、$N$、$P$、$Q$共线,$PQ$与上边界平行且相距为$\dfrac{7}{4}R$,$M$、$N$之间放置足够长的照相底片,包含边界在内该区域存在方向垂直纸面向里的匀强磁场。粒子源发射出质量为$m$、电荷量为$+q$的粒子恰能沿直线通过速度选择器,并从距离$P$点$\dfrac{1}{2}R$的小空隙$O$竖直向上射入磁场区域,并全部打在照相底片上。已知速度选择器中磁感应强度大小为$B$,电场强度大小为$E$,不计粒子重力,求∶
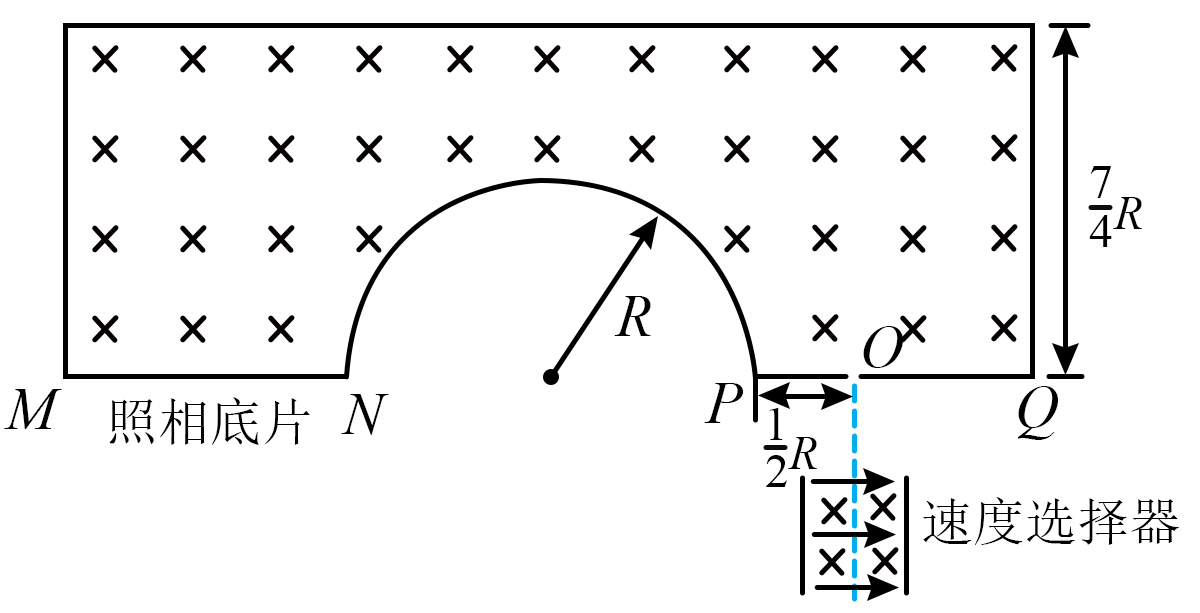
粒子进入有界磁场区域时的速度大小;
$v= \\dfrac{E}{B}$
"]]粒子通过速度选择器,电场力和洛伦兹力平衡,得$qvB=qE$
解得$v=\dfrac{E}{B}$
有界磁场区域所加磁场的磁感应强度的大小范围。
$\\dfrac{4mE}{7qRB} \\leqslant B_{0} \\leqslant \\dfrac{4mE}{5qRB}$
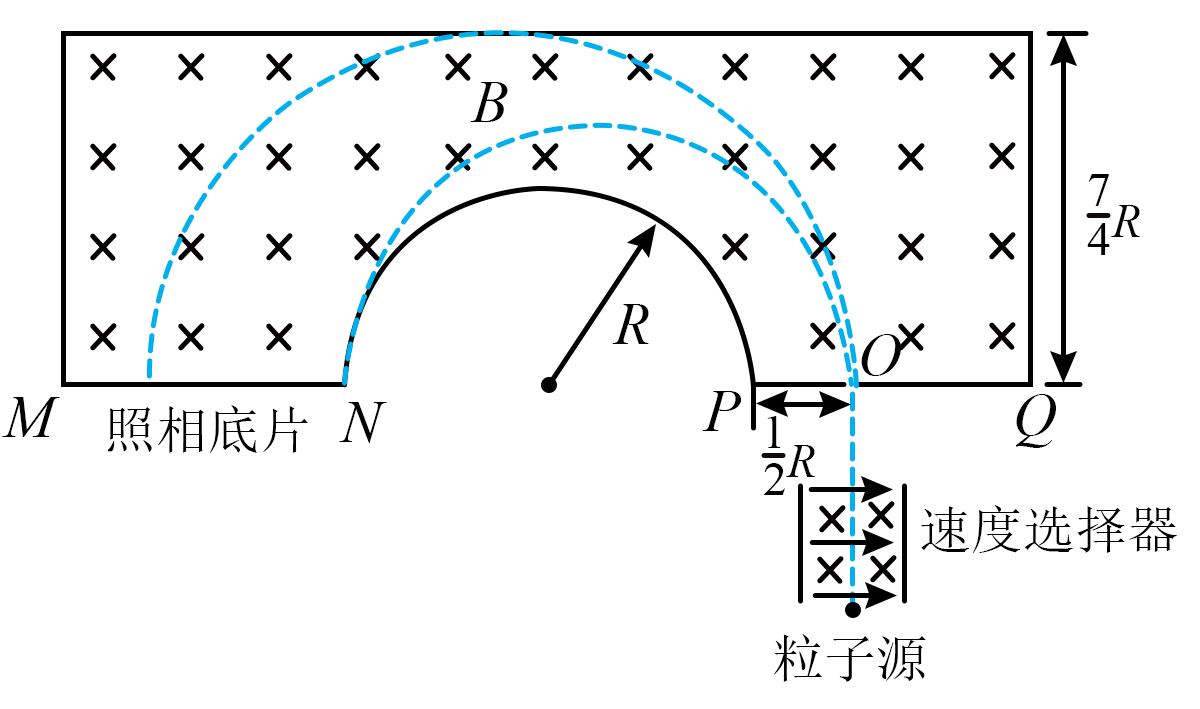
"]]若粒子打在$N$点,如图所示,由几何关系得$r_{1}=\dfrac{2R+\dfrac{1}{2}R}{2}=\dfrac{5}{4}R$
又$qvB_{1}=m\dfrac{v^{2}}{r_{1}}$
解得$B_{1}=\dfrac{4mE}{5qRB}$,$r_{2}=\dfrac{7}{4}R$
又$qvB_{2}=m\dfrac{v^{2}}{r_{2}}$
解得$B_{2}=\dfrac{4mE}{7qRB}$
磁感应强度$B$的大小范围为$\dfrac{4mE}{7qRB} \leqslant B_{0} \leqslant\dfrac{4mE}{5qRB}$
高中 | 洛伦兹力题目答案及解析(完整版)
