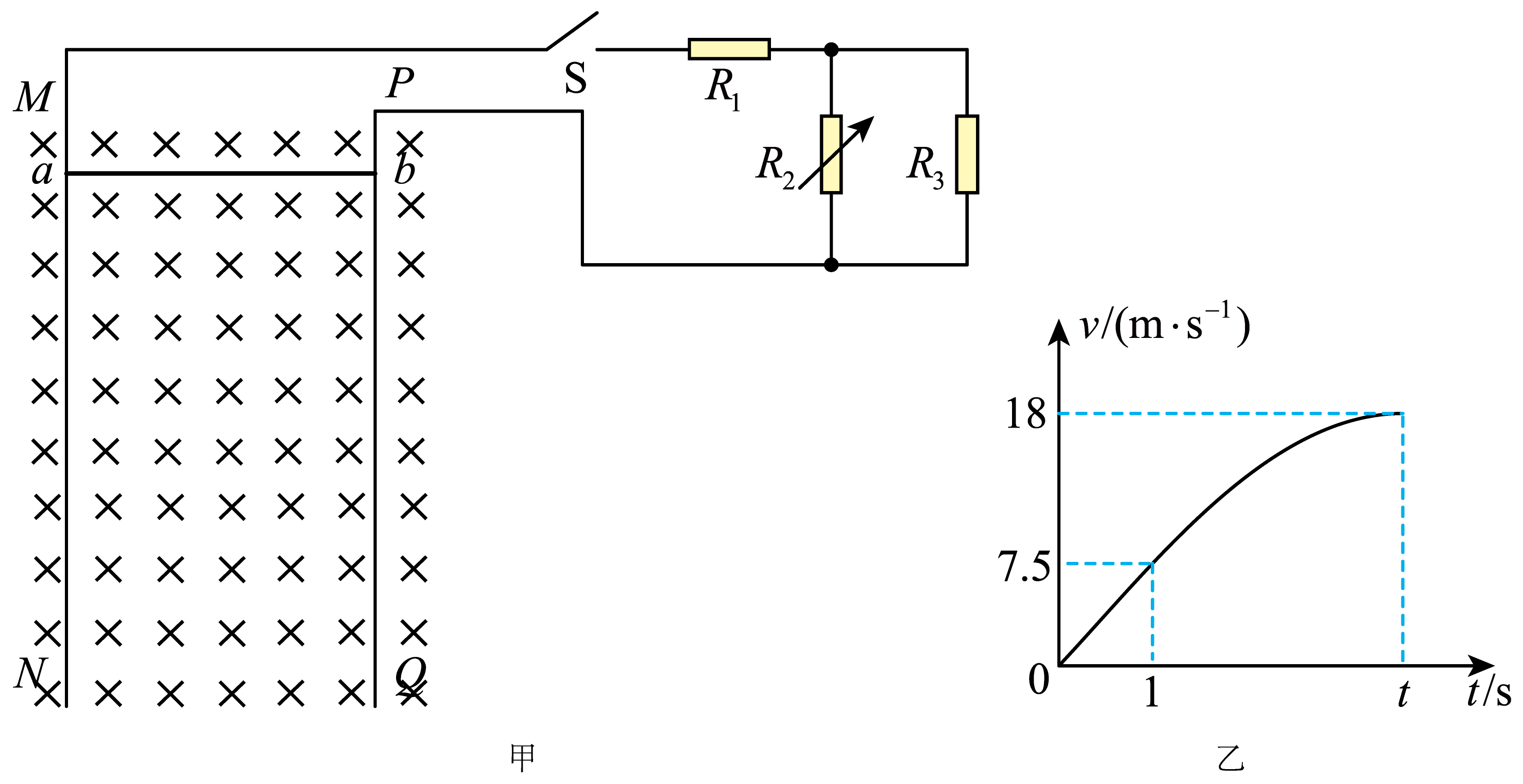
求匀强磁场的磁感应强度大小；

$0.5\\;\\rm T$

设该星球表面的重力加速度为$g$，开关$\rm S$打开，对金属棒受力分析及从图上得，在$0\sim1\;\rm s$内金属棒的加速度为$a=g=\dfrac{\Delta v}{\Delta t}=7.5\;\rm \text{m/s}^{2}$

金属棒匀速下滑时速度最大，此时棒所受的安培力为$F_{安}=BIL$，$I=\dfrac{BLv_{{m}}}{R}$，$R=r+R_{1}+\dfrac{R_{2}R_{3}}{R_{2}+R_{3}}=6\;\rm \Omega$

从图上得$v_{m}=18\;\rm m/s$

由平衡条件得$mg=F_{安}$

所以$mg=\dfrac{B^{2}L^{2}v_{{m}}}{R}$

代入数据解得$B=0.5\;\rm T$

求图像中$t$的数值及$t$时间内整个电路产生的焦耳热；（结果均保留一位小数）

$5.1\\;\\rm s$，$27.1\\;\\rm J$

闭合开关后，由动量定理可得$mg⋅\Delta t-BIL⋅\Delta t=mv_{m}-mv$

$q=I⋅\Delta t$

由法拉第电磁感应定律及闭合电路欧姆定律可得$E=\dfrac{BLh}{\Delta t}$

$q=\dfrac{E}{R}\cdot \Delta t$

联立可得$\Delta t=\dfrac{\dfrac{B^{2}L^{2}h}{R}+mv_{{m}}-mv}{mg}=4.1\;\rm \text{s}$

所以$t=\Delta t+1=5.1\;\rm s$

金属棒由静止开始下滑到最大速度的过程，由动能定理得$mg(h+x)-Q=\dfrac{1}{2}mv_{{m}}^{2}-0$，$x=\dfrac{1}{2}vt'=\dfrac{7.5}{2}\;\text{m}$

解得$Q=mg(h+x)-\dfrac{1}{2}mv_{{m}}^{2} \approx 27.1\;\rm \text{J}$

电阻箱$R_{2}$取何值时，金属棒再次匀速下滑且$R_{2}$消耗的功率最大。

$4\\;\\rm \\Omega$

改变电阻箱$R_{2}$的值后，电阻值为$R_{2}^\prime$，金属棒匀速下滑时满足

$mg=BI'L$$R_{2}$两端的电压为$U=I'\left(\dfrac{{R_{2}'}R_{3}}{{R_{2}'}+R_{3}}\right)$

$R_{2}$消耗的功率为$P_{2}=\dfrac{U^{2}}{R''_{2}}$

由上联立解得$P_{2}=\left( \dfrac{mg}{BL} \right)^{2}\dfrac{\left( \dfrac{{R_{2}''}R_{3}}{{R_{2}''}+R_{3}} \right)^{2}}{{R_{2}''}}=\dfrac{36}{\dfrac{16}{{R_{2}''}}+{R_{2}''}+8}$

由数学知识得，当$\dfrac{16}{{R_{2}''}}={R_{2}''}$

即$R_{2}''=4\;\rm \Omega$

$R_{2}$消耗的功率最大。