| 带电粒子在等效重力场中的运动 题目答案及解析
稿件来源:高途
| 带电粒子在等效重力场中的运动题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
带电粒子在等效重力场中的运动
如图所示,有一带电物块(可视为质点)静止在光滑斜面的 $S$ 处,物块的电荷量$q=1.0 \times 10^{-4}\;\rm C$,质量 $m=0.20\;\rm kg$,斜面的倾角为$37^\circ$。斜面与水平绝缘轨道 $AB$平滑,在直线$AM$ 左侧有水平向左的匀强电场$E_{1}$,$AM$ 右侧有水平向右的匀强电场$E_{2}=2.0 \times 10^{4}\;\rm N/C$,水平轨道 $AB$ 与竖直平面内的半圆形绝缘光滑轨道 $BC$ 平滑连接,半圆形轨道的半径$R=0.9\;\rm m$。现撤去电场$E_{1}$,物块从 $S$ 处由静止下滑,恰好能通过半圆形轨道的最高点 $C$,然后落至水平轨道 $AB$上。已知$S$ 距离水平轨道的高度为$h_{1}=0.8\;\rm m$,带电物块与 $AB$ 间的动摩擦因数为 $0.5$,取 $g=10\;\rm m/s^{2}$,求:
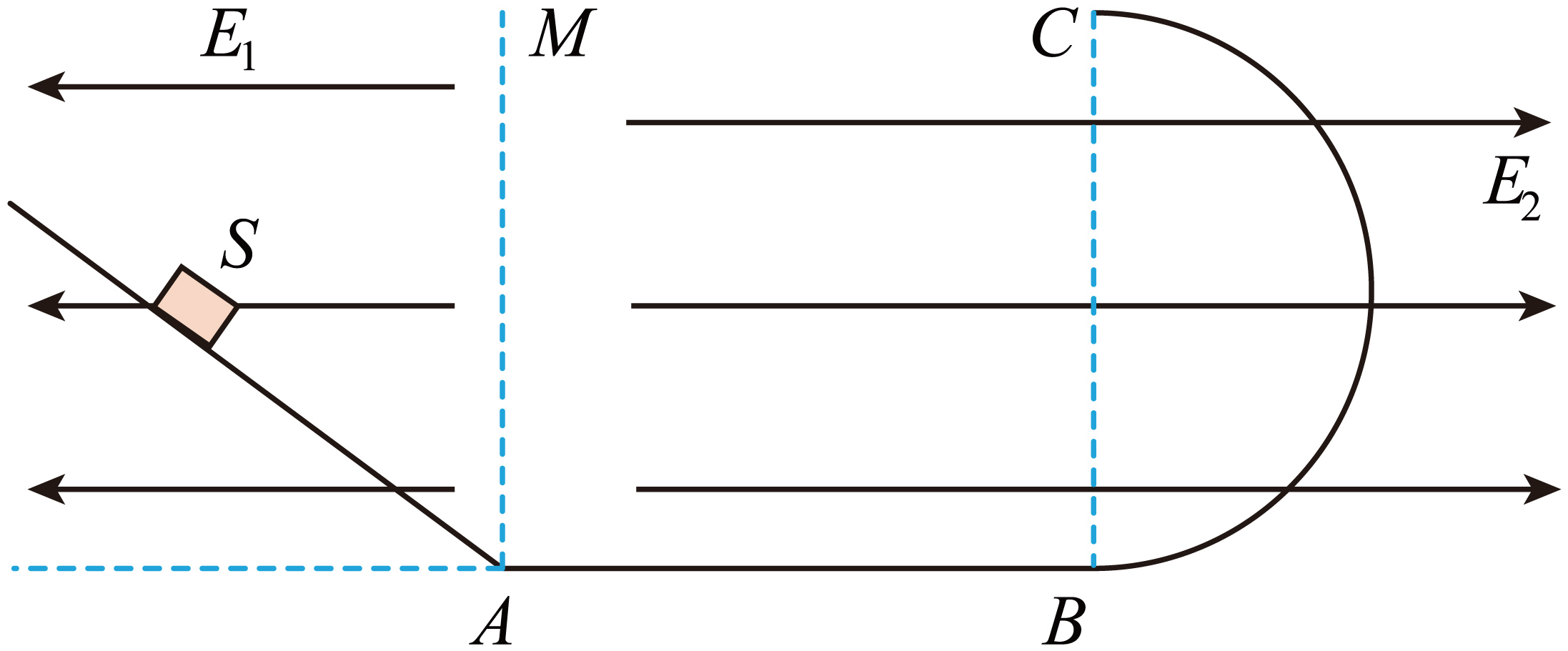
匀强电场$E_{1}$的大小;
$1.5 \\times 10^{4}\\;\\rm N/C$;
"]]根据$S$在斜面上受力平衡,则有$F=qE_{1}=mg\tan 37^\circ $
解得$E_{1}=1.5 \times 10^{4}\;\rm N/C$;
$AB$ 间的距离。
$2.9\\;\\rm m$。
"]]已知物块在$S$处的初速度为$0$,并且恰好能够通过最高点$C$,则$mg=m\dfrac{{v_{C}}^{2}}{R}$
解得在$C$点处的速度为$v_{C}=\sqrt{gR}=3\;\rm m/s$
由$S$到$C$点整个过程中有重力、摩擦力以及电场力三个力做功,设$AB$ 段长度为$x$,则有
$W_{f}=−\mu mgx$,$W_{E}=E_{2}qx$
由题目条件可知,$S$与$C$之间的高度差为$\Delta h=1\;\rm m$
因此有重力做功为$W_{G}=−mg\Delta h$
利用动能定理有$W_{E}+W_{G}+W_{f}=\dfrac{1}{2}m{v_{C}}^{2}-\dfrac{1}{2}m{v_{S}}^{2}$
解得$x=2.9\;\rm m$。
| 带电粒子在等效重力场中的运动题目答案及解析(完整版)
