如图甲所示，光滑斜面底端有一固定挡板，轻质弹簧一端固定在挡板上，质量为$m$的物块$\rm P$（可视为质点）从斜面上的$O$点由静止释放，$\rm P$的加速度大小$a$随它与$O$点的距离$x$变化的关系如图乙所示，图乙中各坐标值均已知，${{x}_{3}}$为物块$\rm P$到$O$点的最大距离，弹簧始终处于弹性限度内。下列说法正确的是$(\quad\ \ \ \ )$

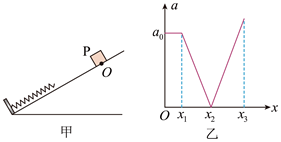
$x={{x}_{1}}$时，物块$\\rm P$速度最大

物块$\\rm P$运动过程中的最大加速度为$\\dfrac{\\left( {{x}_{3}}-{{x}_{2}} \\right){{a}_{0}}}{{{x}_{2}}-{{x}_{1}}}$

弹簧的最大弹性势能为$m{{a}_{0}}{{x}_{3}}$

物块$\\rm P$的最大动能为$\\dfrac{1}{2}m{{a}_{0}}\\left( {{x}_{1}}+{{x}_{2}} \\right)$

$A$．在物块沿斜面向下运动的过程中，对物块$P$进行分析可知，物块先向下做匀加速直线运动，与弹簧接触后，先向下做加速度减小的加速运动，当加速度减小为$0$时，速度达到最大值，之后再向下做加速度方向变为向上的变减速直线运动，可知$x={{x}_{2}}$时，物块$P$速度最大，故$A$错误；

$B$．物块$P$没有接触弹簧前，对物块分析有$mg\text{sin}\theta =m{{a}_{0}}$

在$x={{x}_{2}}$时，加速度为$0$，则有$k\left( {{x}_{2}}-{{x}_{1}} \right)=mg\text{sin}\theta $

在$x={{x}_{3}}$时，物块的加速度最大，此时有$k\left( {{x}_{3}}-{{x}_{1}} \right)-mg\text{sin}\theta =m{a}'$

解得${a}'=\dfrac{\left( {{x}_{3}}-{{x}_{2}} \right){{a}_{0}}}{{{x}_{2}}-{{x}_{1}}}$

故$B$正确；

$C$．物块$P$没有接触弹簧前，对物块分析有$mg\text{sin}\theta =m{{a}_{0}}$

由于${{x}_{3}}$为物块$P$到$O$点的最大距离，即在$x={{x}_{3}}$时，物块的速度为$0$，根据能量守恒定律可知，弹簧的最大弹性势能为${{E}_{\text{pmax}}}=mg{{x}_{3}}\text{sin}\theta =m{{a}_{0}}{{x}_{3}}$

故$C$正确；

$D$．根据上述可知，$x={{x}_{2}}$时，物块$P$速度最大，动能最大，根据动能定理有$mg{{x}_{2}}\text{sin}\theta +{{W}_{}}={{E}_{\text{kmax}}}$

根据胡克定律可知，弹簧弹力与形变量成正比，利用弹力的平均值可以得到${{W}_{}}=-\dfrac{k{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}}{2}$

由于在$x={{x}_{2}}$时，加速度为$0$，则有$k\left( {{x}_{2}}-{{x}_{1}} \right)=mg\text{sin}\theta $

解得${{E}_{\text{kmax}}}=\dfrac{1}{2}m{{a}_{0}}\left( {{x}_{1}}+{{x}_{2}} \right)$

故$D$正确。

故选$BCD$。