高中 | 功率的概念与计算 题目答案及解析
稿件来源:高途
高中 | 功率的概念与计算题目答案及解析如下,仅供参考!
必修2
第七章 机械能守恒定律
7.3 功率
功率的概念与计算
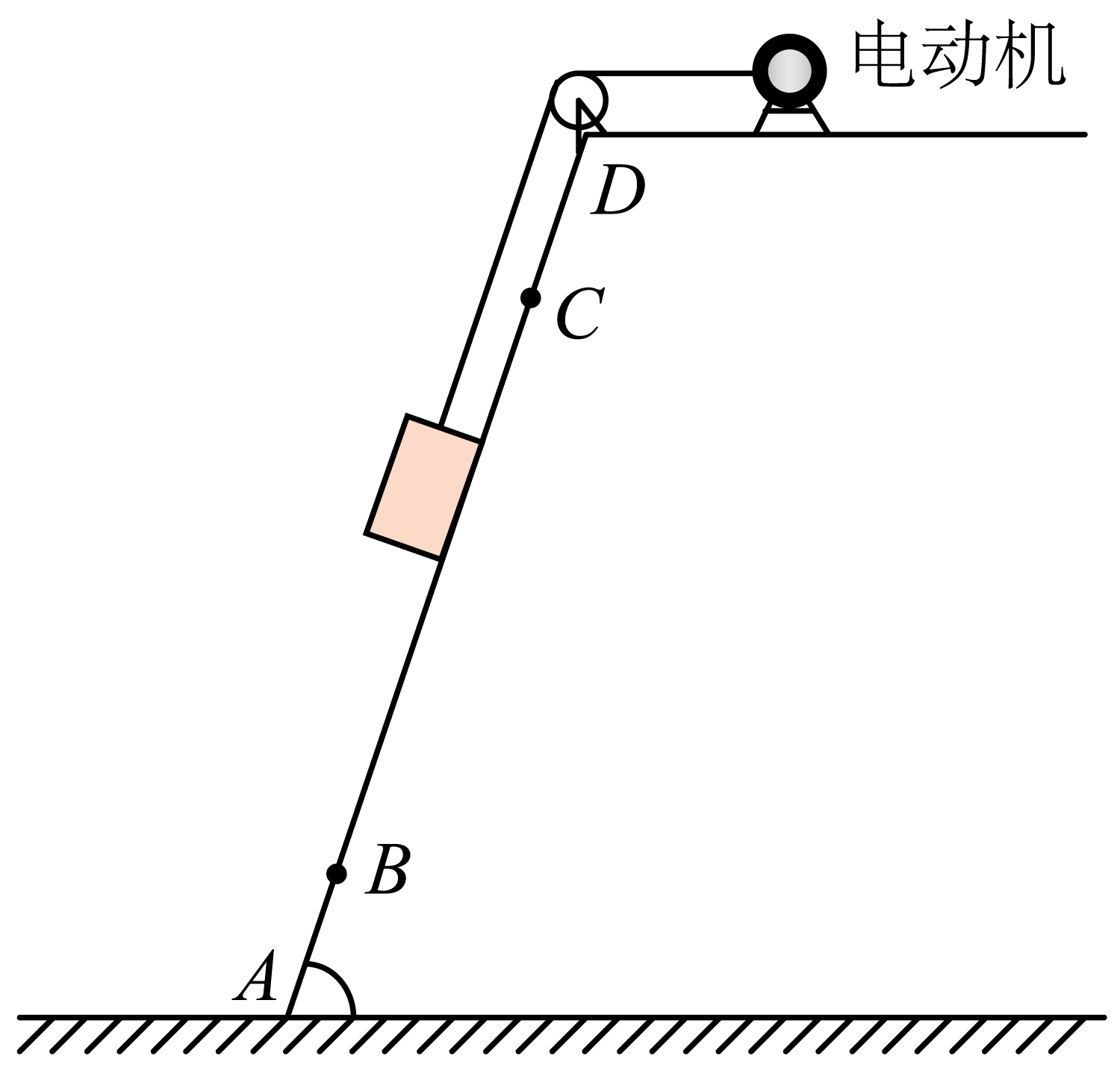
某重力储能系统的简化模型如图所示,长度为$L$、倾角为$\theta$的斜坡$ABCD$上,有一质量为$m$的重物通过线索与电动机连接。在电动机的牵引下,重物从斜坡底端$A$点由静止开始运动,到达$B$点时速度达到最大值$v$,然后重物被匀速拉到$C$点,此时关闭电动机,重物恰好能滑至顶端$D$点,系统储存机械能。已知绳索与斜坡平行,重物与斜坡间的动摩擦因数为$\mu $,重力加速度为$g$,不计空气阻力和滑轮摩擦。
求$CD$的长度$x$;
$\\dfrac{v^{2}}{2g\\left( \\sin\\theta+\\mu\\cos\\theta \\right)}$;
"]]重物在$CD$段运动过程中,由牛顿第二定律得$mg\sin \theta+\mu mg\cos \theta=ma$
由运动学公式$0 − v^{2}=-2ax$
联立解得$x=\dfrac{v^{2}}{2g\left( \sin\theta+\mu\cos\theta \right)}$;
求重物从$B$到$C$过程中,电动机的输出功率$P$;
$mgv(\\sin \\theta+\\mu \\cos \\theta)$;
"]]重物在$BC$段匀速运动,得电动机的牵引力为$F=mg\sin \theta+\mu mg\cos \theta$
由$P=Fv$得$P=mgv(\sin \theta+\mu \cos \theta)$;
若不计电动机的损耗,取在整个上升过程中,系统存储的机械能$E_{1}$和电动机消耗的电能 $E_{2}$的比值。
$\\dfrac{\\sin\\theta}{\\sin\\theta+ \\mu\\cos\\theta}$。
"]]全过程重物增加的机械能为$E_{1}=mgL\sin \theta$
整个过程由能量守恒得电动机消耗的总电能转化为重物增加的机械能和摩擦产生的内能,故可知$E_{2}=E_{1}+\mu mg\cos \theta ⋅ L$
故可得$\dfrac{E_{1}}{E_{2}}=\dfrac{mgL\sin\theta}{mgL\sin\theta+\mu mgL\cos\theta}=\dfrac{\sin\theta}{\sin\theta+\mu\cos\theta}$。
高中 | 功率的概念与计算题目答案及解析(完整版)
