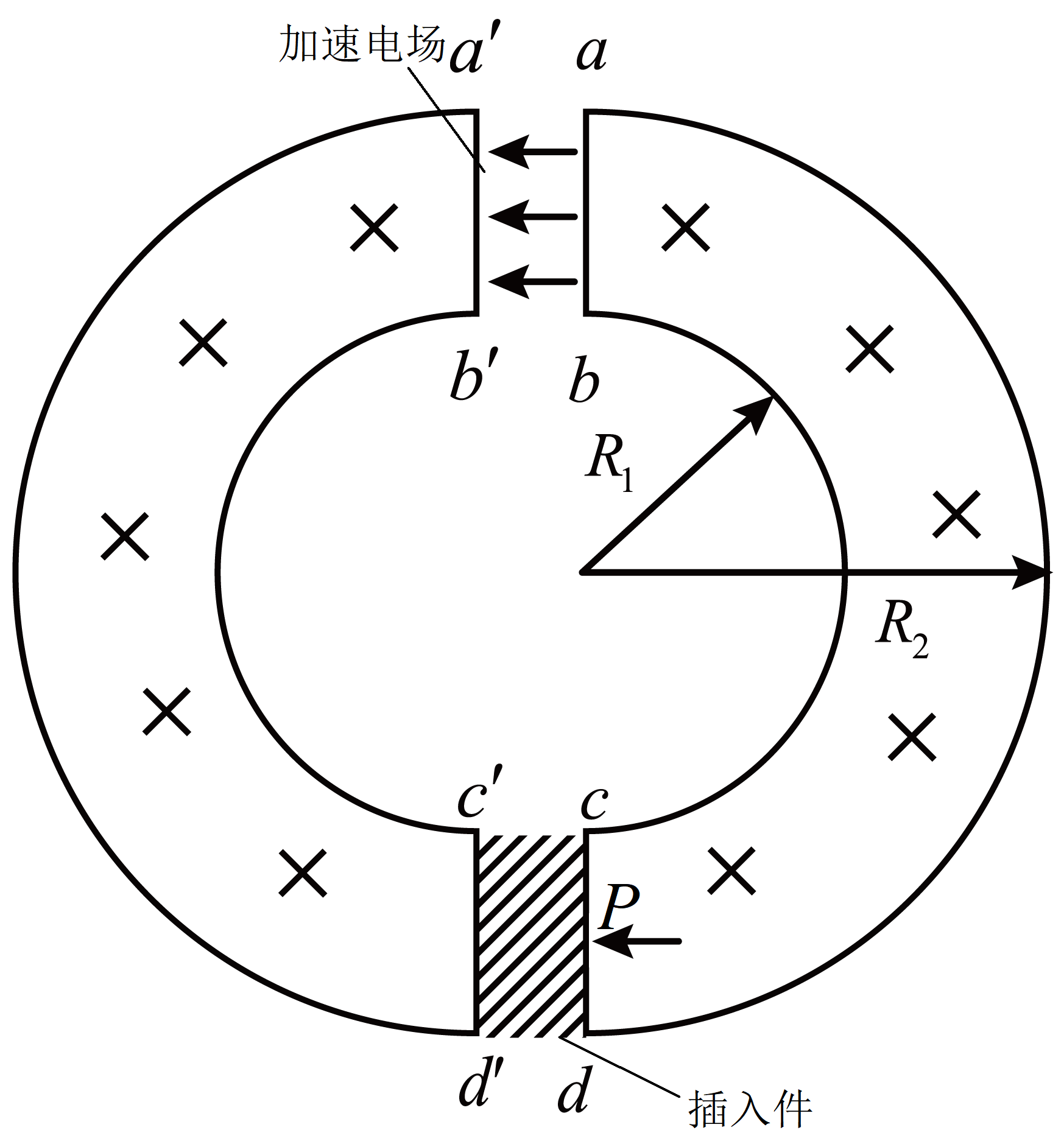
求该电子进入插入件前、后，在磁场中运动的半径之比$r_{1}:r_{2}$；

$1:k$；

设电子进入插入件前后的速度大小分别为$v_{1}$、$v_{2}$，由题意可得$v_{2}=kv_{1}$

电子在磁场中做匀速圆周运动，由洛伦兹力提供向心力得$evB=m\dfrac{v^{2}}{r}$

解得$r=\dfrac{mv}{eB}$

可知在磁场中的运动半径$r ∝ v$，可得$r_{1}:r_{2}=v_{1}:v_{2}=1:k$；

求该电子多次循环后到达$cd$的稳定速度$v$；

$\\sqrt{\\dfrac{2eU}{m(1- k^{2})}}$，方向垂直于$cd$向左；

电子多次循环后到达$cd$的稳定速度大小为$v$，则经过插入件后的速度大小为$kv$。电子经过电场加速后速度大小为$v$，根据动能定理得$eU=\dfrac{1}{2}mv^{2}-\dfrac{1}{2}m{(kv)}^{2}$

解得$v=\sqrt{\dfrac{2eU}{m(1-k^{2})}}$

方向垂直于$cd$向左；

若该电子运动到$cd$的中点$P$时达到稳定速度，并最终能到达边界的$d$点，求电子从$P$点运动到$d$的时间$t$。

$\\dfrac{\\pi(R_{2}- R_{1})}{2}\\sqrt{\\dfrac{m(1+k)}{2eU(1-k)}}$。

电子到达$cd$中点$P$时速度稳定，并最终到达边界上的$d$点，

由Р点开始相继在两个半圆区域的运动轨迹如下图所示：

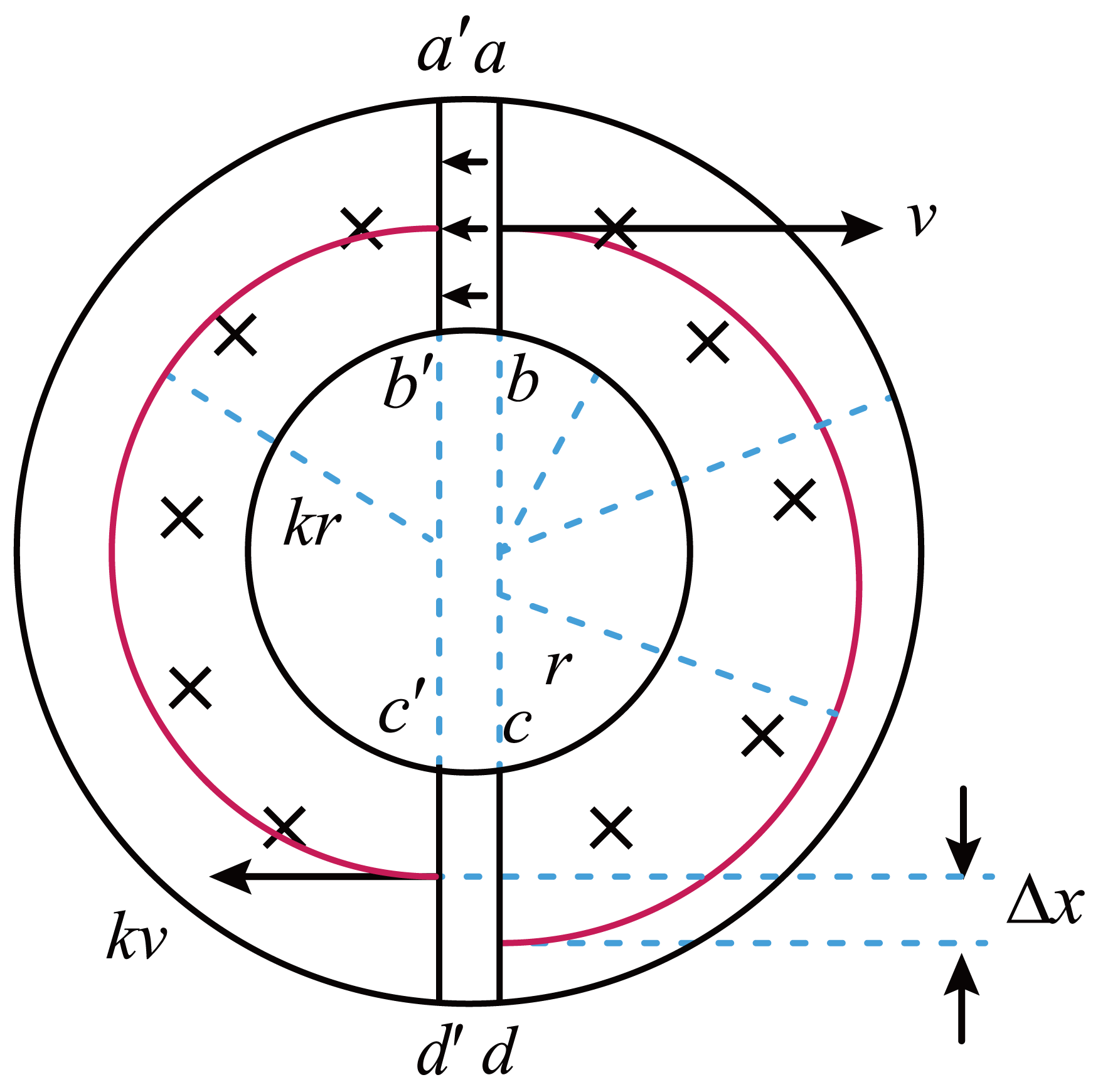
根据$(1)$$(2)$的结论，可得电子在右半圆区域的运动半径为$r=\dfrac{mv}{eB}=\dfrac{1}{B}\sqrt{\dfrac{2mU}{e(1-k^{2})}}$

电子在左半圆区域的运动半径为$kr$，则$\Delta x=2r − 2kr$$P$点与$d$点之间的距离为$\overline{Pd}=\dfrac{1}{2}(R_{2}-R_{1})$

电子由Р点多次循环后到达$d$点的循环次数为$n=\dfrac{\overline{Pd}}{\Delta x}=\dfrac{R_{2}-R_{1}}{4(1-k)r}$

电子在左、右半圆区域的运动周期均为$T=\dfrac{2\pi m}{eB}$

忽略经过电场与插入体的时间，则每一次循环的时间均等于$T$，可得电子从Р到$d$的时间为$t=nT=\dfrac{\pi(R_{2}-R_{1})}{2}\sqrt{\dfrac{m(1+k)}{2eU(1-k)}}$。