如图所示，真空中水平正对放置的两块带电金属板，板间形成匀强电场，电场强度大小为$E$，板间同时存在与匀强电场正交的匀强磁场，磁感应强度大小为$B_{0}$，方向垂直于纸面向里。金属板右端以$O$为圆心的圆形区域内存在另一方向垂直于纸面向里的匀强磁场，磁感应强度大小为$B$。一带电粒子从$A$点射入金属板间，沿直线$AC$运动，从$F$点射出。已知$CD$为直径，长度为$\dfrac{2\sqrt{3}}{3}L$，$OF$与$OD$夹角为$60^\circ $，不计粒子重力。则$(\qquad)$

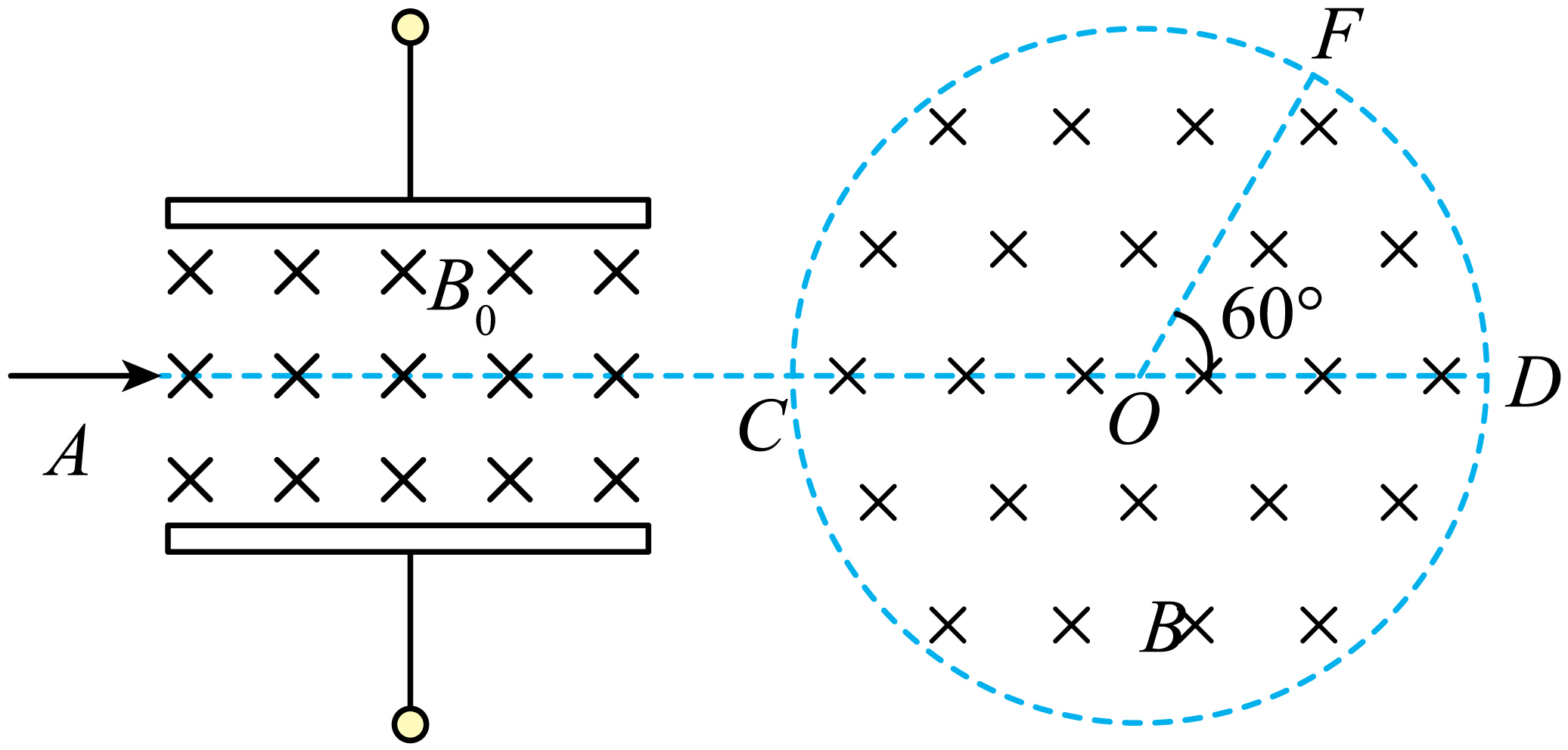
粒子一定带负电

粒子速度的大小为$\\dfrac{B_{0}}{E}$

粒子的比荷为$\\dfrac{E}{2B_{0}BL}$

粒子在圆形区域中运动时间为$\\dfrac{\\pi B_{0}L}{3E}$

$\rm A$．带电粒子从$A$点射入金属板间，沿直线$AC$运动，从$F$点射出，则带电粒子在磁场中受力向上，由左手定则可知粒子一定带正电，故$\rm A$错误；

$\rm B$．带电粒子在两块带电金属板间沿直线$AC$运动，所受电场力与磁场力大小相等，方向相反$qE=qvB_{0}$

则粒子速度的大小为$v=\dfrac{E}{B_{0}}$

故$\rm B$错误；

$\rm C$．由题意可知圆形磁场的半径$R=\dfrac{1}{2}CD=\dfrac{\sqrt{3}}{3}L$

如图所示

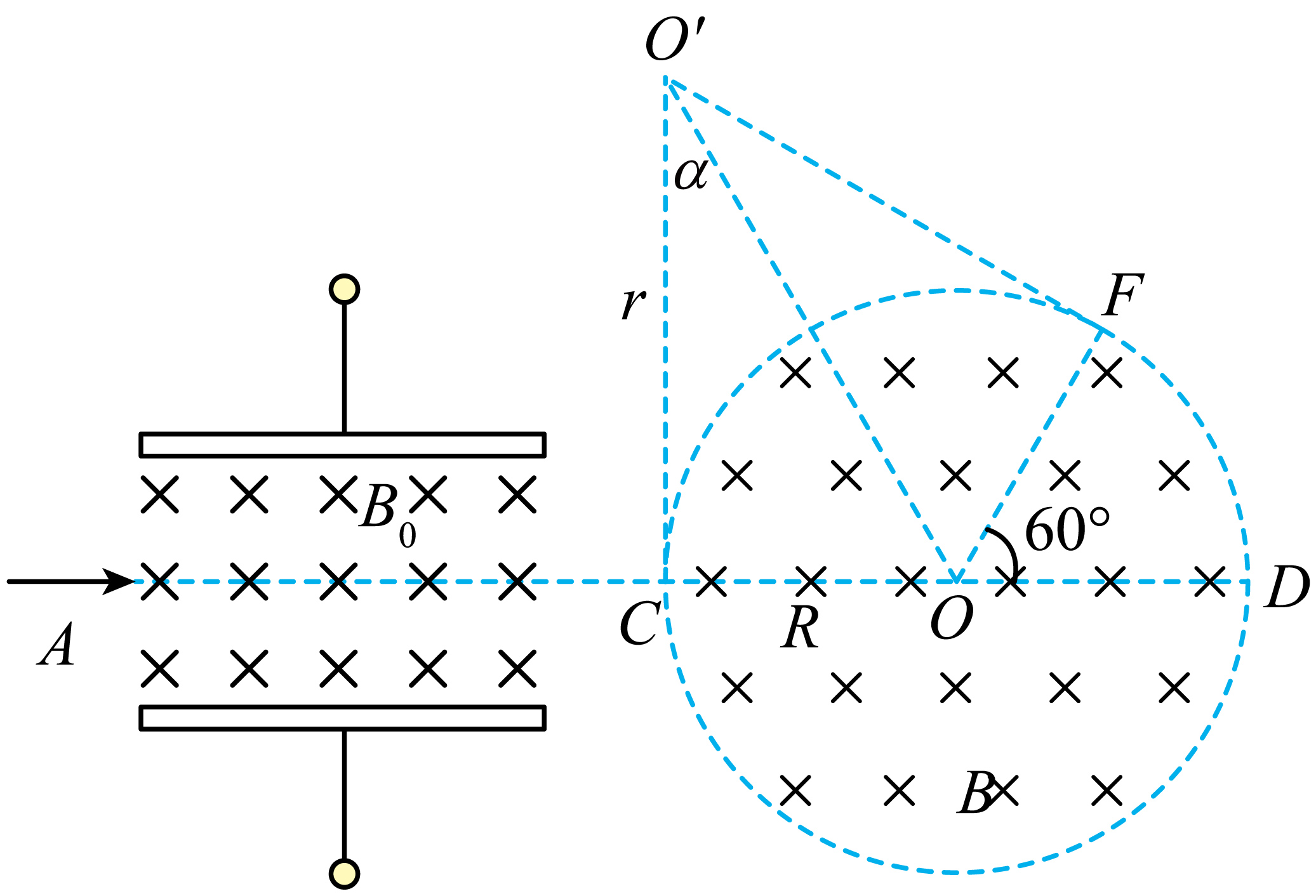
由几何知识可知带电粒子在磁场中运动轨迹的半径$r=\dfrac{R}{\tan\alpha}=\dfrac{R}{\tan 30^\circ}=L$

由牛顿第二定律得$qvB=m\dfrac{v^{2}}{r}$，解得$\dfrac{q}{m}=\dfrac{v}{Br}=\dfrac{E}{B_{0}BL}$

故$\rm C$错误；

$\rm D$．由周期公式$T=\dfrac{2\pi r}{v}$，可得$T=\dfrac{2\pi m}{qB}=\dfrac{2\pi B_{0}L}{E}$

粒子在圆形区域中运动时间为$t=\dfrac{\angle CO'F}{360^\circ}T=\dfrac{1}{6}T=\dfrac{\pi B_{0}L}{3E}$

故$\rm D$正确。

故选：$\rm D$。