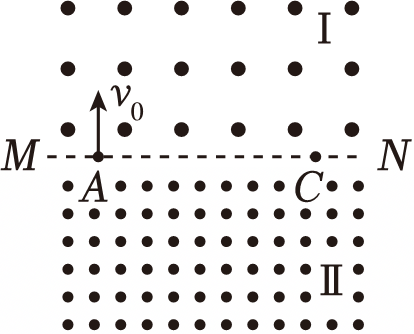
如图所示，空间存在着两个方向均垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ，磁感应强度大小分别为$B_{1}$、$B_{2}$，且$B_{1}=B_{0}$、$B_{2}=4B_{0}$，$MN$为两个磁场的边界。一质量为$m$、电荷量为$q$的带正电粒子（不计重力）从边界上的$A$点以一定的初速度垂直$MN$竖直向上射入匀强磁场区域Ⅰ中，边界$MN$上的$C$点与$A$点的距离为$d$。若粒子恰能经过$C$点，则该粒子从$A$点射入磁场的速度$v_{0}$大小可能为$(\quad\ \ \ \ )$

$\\dfrac{dqB_{0}}{8m}$

$\\dfrac{dqB_{0}}{2m}$

$\\dfrac{2dqB_{0}}{3m}$

$\\dfrac{dqB_{0}}{m}$

粒子在磁场中做匀速圆周运动，由洛伦兹力提供向心力得：

$qBv_{0}=m\dfrac{v_0^2}{r}$

解得圆周运动半径为：$r=\dfrac{mv_0}{qB}$

设粒子在区域Ⅰ中的半径为$r_{1}$，在区域Ⅱ中的半径为$r_{2}$，可得：

${r}_{1}=\dfrac{m{v}_{0}}{q{B}_{0}}$，${r}_{2}=\dfrac{m{v}_{0}}{4q{B}_{0}}$

可得：$r_{1}=4r_{2}$

粒子的运动轨迹如下图所示，轨迹与分界线$MN$的交点为$C_{1}$、$C2$、$C_{3}$、$C_{4}$、$\cdots \cdots$

当$C_{1}$、$C_{3}$、$C_{5}$、$C_{7}$、$\cdots \cdots$作为$C$点时，需满足：

$n(2r_{1}-2r_{2})=d$

联立解得：$r_{1}=\dfrac{2d}{3n}$，$n=1$、$2$、$3\cdots \cdots$

此时可得：$v_{0}=\dfrac{2dqB_0}{3nm}$

当$n=1$时，$v_{0}=\dfrac{2dqB_0}{3m}$

当$C_{2}$、$C_{4}$、$C_{6}$、$C_{8}$、$\cdots \cdots$作为$C$点时，需满足：

$2r_{1}+k(2r_{1}-2r_{2})=d$

联立解得：$r_{1}=\dfrac{2d}{4+3k}$，$k=0$、$1$、$2$、$3\cdots \cdots$

此时可得：$v_{0}=\dfrac{2dqB_0}{(4+3k)m}$

当$k=0$时，$v_{0}=\dfrac{dqB_0}{2m}$；当$k=4$时，$v_{0}=\dfrac{dqB_0}{8m}$

综上所述，可知$ABC$正确，$D$错误。

故选：$ABC$。