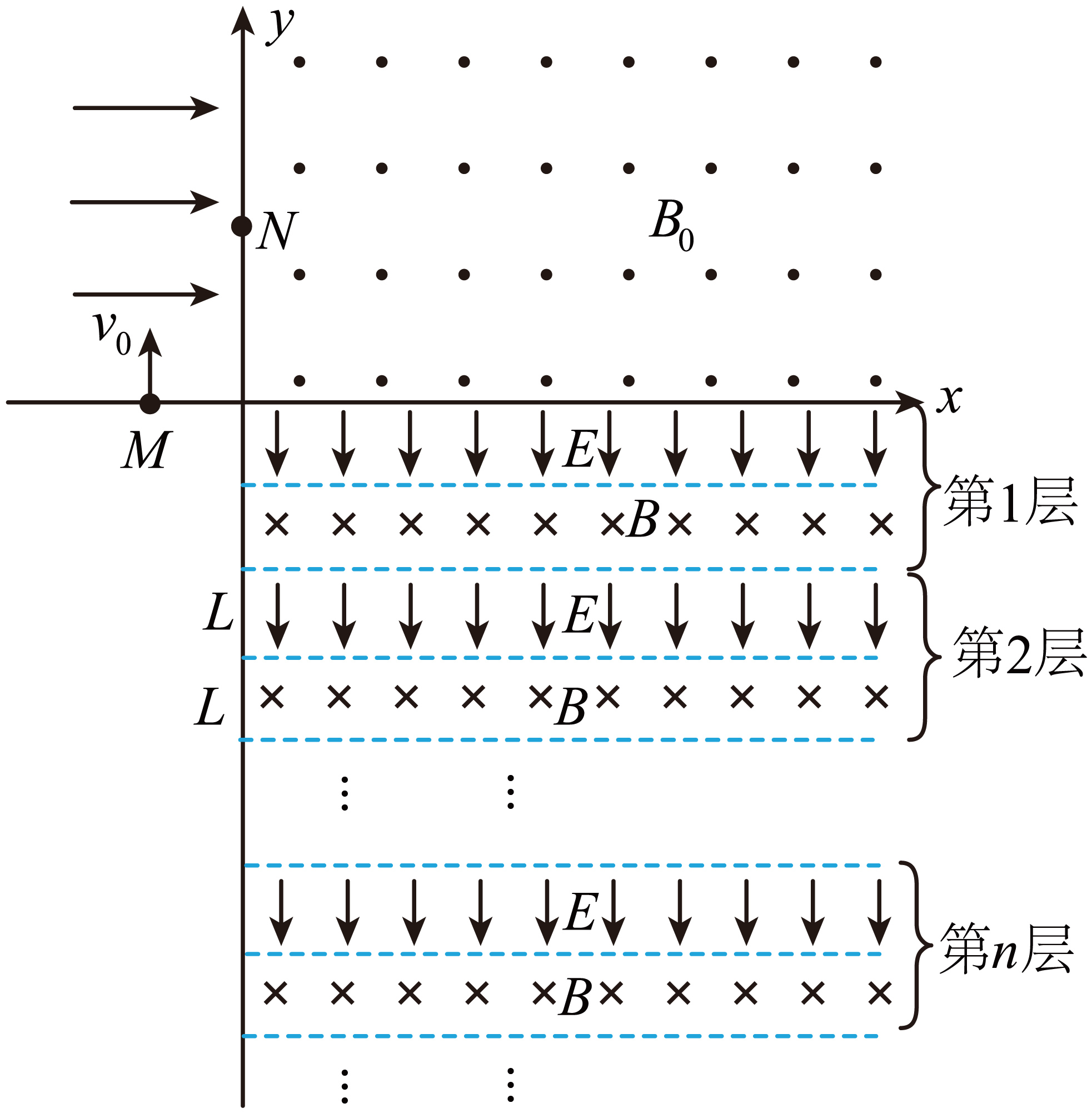
磁感应强度$B_{0}$的大小；

$B_{0}= \\dfrac{mv_{0}}{2qL}$；

设粒子在第$II$象限运动的时间为$t$，在$N$点沿$x$轴的分速度为$v_{x}$，由于粒子垂直电场方向进入电场则可知粒子在电场中做类平抛运动，由平抛运动的研究方法，$x$方向有$L=\dfrac{v_{x}}{2}t$

$y$方向有$2L=v_{0}t$

通过$N$点的速度$v_{N}=\sqrt{v_{x}^{2}+v_{0}^{2}}=\sqrt{2}v_{0}$

与$y$轴正方向的夹角满足$\tan \alpha=1$

在第$I$象限运动由牛顿第二定律有$qv_{N}B_{0}=m\dfrac{v_{N}^{2}}{R}$

根据垂直于$x$轴进入第$IV$象限，由几何关系知$R=2\sqrt{2}L$

联立解得$B_{0}=\dfrac{mv_{0}}{2qL}$；

粒子刚射出第$1$层磁场下边界时的速度方向；

与$y$轴负方向夹角为$30^\\circ$；

设穿过$x$轴下方第一层电场后的速度为$v_{1}$，由动能定理有$EqL=\dfrac{1}{2}mv_{1}^{2}- \dfrac{1}{2}mv_{N}^{2}$

解得$v_{1}=\sqrt{6}v_{0}$

在$x$轴下方第一层磁场中运动的轨迹如图所示

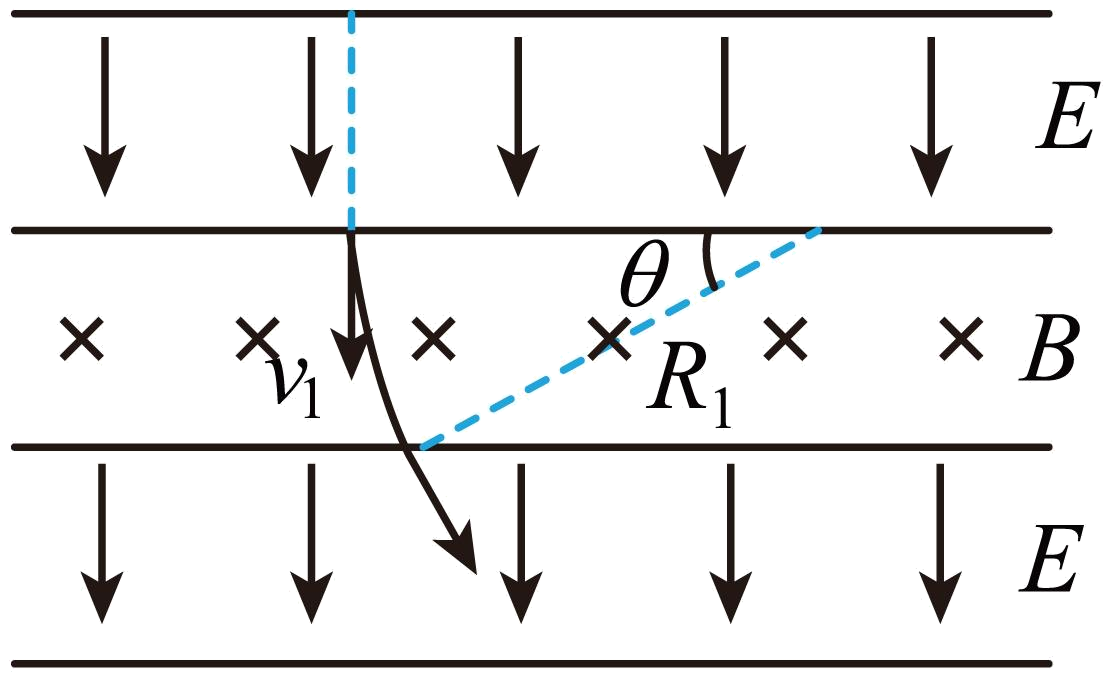
由洛伦兹力充当向心力有$Bqv_{1}=m\dfrac{v_{1}^{2}}{R_{1}}$

解得$R_{1}=2L$

设速度偏转角为$\theta$，则根据几何关系可得$\sin\theta=\dfrac{L}{R_{1}}=\dfrac{1}{2}$

则$\theta=30^\circ $

即粒子射出第$1$层磁场下边界时速度的方向与$y$轴负方向夹角为$30^\circ$；

粒子进入第$n$层磁场时的速度大小$v_{n}$以及最远能进入第几层磁场。

$v_{n}=\\sqrt{2+ 4n}v_{0}$，$4$。

当粒子在第$n$层磁场中运动时，此前粒子已经过$n$个电场，

由动能定理$nEqL=\dfrac{1}{2}mv_{n}^{2}-\dfrac{1}{2}mv_{N}^{2}$

解得$v_{n}=\sqrt{2+4n}v_{0}$

若粒子在第$n$层磁场中距离$x$轴最远，则最大速度为$v_{n}$

在水平方向上由动量定理有$∑qv_{y}B\Delta t=mv_{n} − 0$

即$qBy_{\rm m}=mv_{n}$

其中$y_{\rm m}$为磁场中向下运动的最远距离，由题意$(n − 1)L \lt y_{\rm m} \leqslant nL$

满足条件：$3n^{2} − 8n − 4\geqslant 0$且$3n^{2} − 14n − 1 \lt 0$

解得满足条件的整数$n=4$

故最远能进入第$4$层磁场。