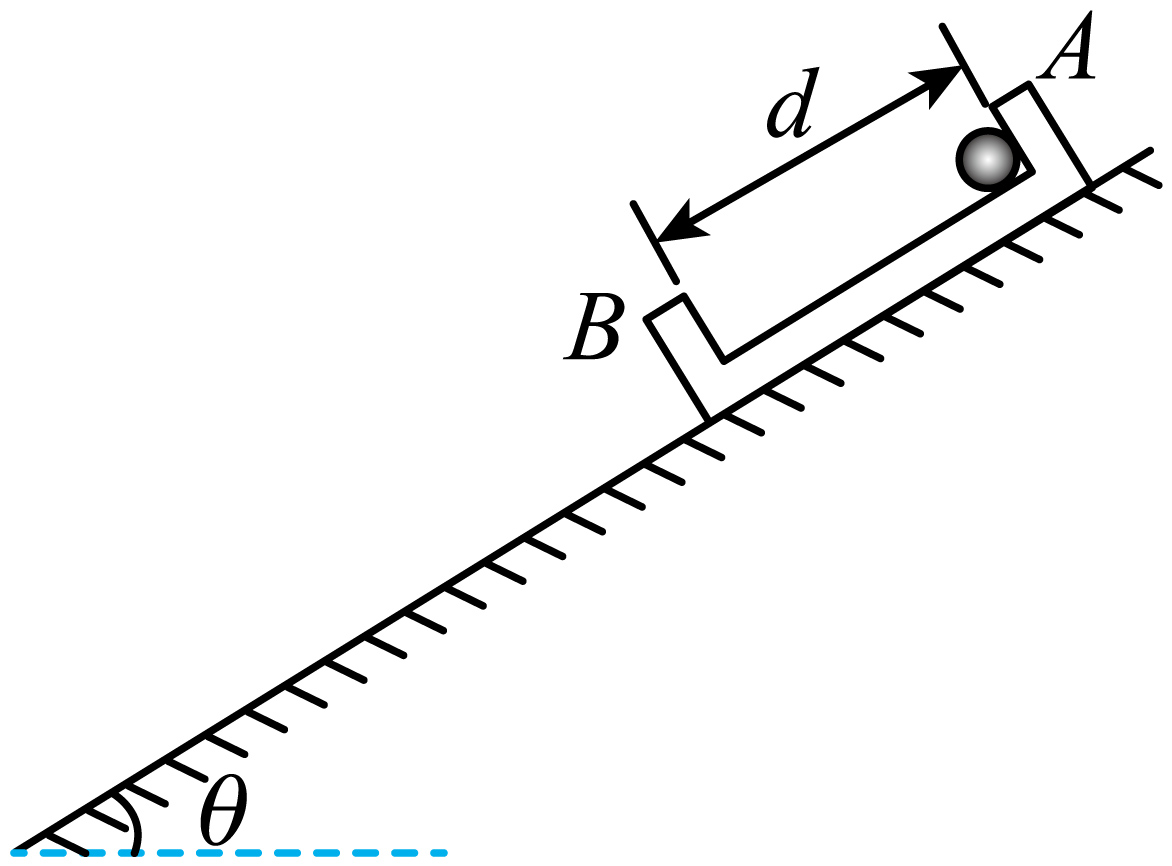
由静止释放球和槽后，经多长时间球与槽的侧壁发生第一次碰撞；

$0.2\\;\\rm s$

对小球根据牛顿第二定律可得$mg\sin37^\circ=ma_{1}$

解得$a_{1}=6\;\rm m/s^{2}$

对槽根据牛顿第二定律可得$mg\sin37^\circ-\mu \cdot 2mg\cos37^\circ=ma_{2}$

解得$a_{2}=0$

根据$d=\dfrac{1}{2}a_{1}{t_{1}}^{2}$

解得$t_{1}=0.2\;\rm s$

第一次碰撞后的瞬间，球和槽的速度；

$0$；$1.2\\;\\rm m/s$

对小球运用运动学公式可得$v^{2}=2a_{1}d$

解得$v=1.2\;\rm m/s$

取沿斜面向下为正方向，根据动量守恒定律可得$mv=mv_{1}+mv_{2}$

根据机械能守恒定律可得$\dfrac{1}{2}mv^{2}=\dfrac{1}{2}m{v_{1}}^{2}+\dfrac{1}{2}m{v_{2}}^{2}$

联立解得小球与槽的侧壁发生第$1$次碰撞后的瞬间，小球和槽的速度大小分别为$v_{1}=0$，$v_{2}=$$1.2\;\rm m/s$

小球第$n$次到达凹槽侧壁所用的时间$t_{n}$。

$(0.4n-0.2)\\;{\\rm s}(n=1,2,3\\cdots)$

小球第一次与槽碰撞经过的时间为$t_{1}$，第一次碰撞后再次与槽碰撞经过的时间为$t_{2}'$，第一次碰撞后槽匀速运动且速度为$v_{2}=1.2\;\rm m/s$，小球匀加速且加速度仍为$a_{1}$，故有$v_{2}{t_{2}'}=\dfrac{1}{2}a_{1}t_{2}'^{2}$

解得$t_{2}'=0.4\;\rm s$

故从小球开始运动至与槽的侧壁发生第$2$次碰撞所需的时间为

$t_{2}=t_{1}+t_{2}'=0.2\;\rm s+0.4\;\rm s=0.6\;\rm s$

第二次碰前小球和槽的速度分别为$2.4\;\rm m/s$和$1.2\;\rm m/s$，碰后两者再次交换速度，即槽的速度为$v_{2}'=2.4\;\rm m/s$，球的速度为$v_{1}'=1.2\;\rm m/s$，碰后第四次碰撞经过的时间为$t_{3}$，则$v_{2}'{t_{3}'}={v_{1}'}{t_{3}'}+\dfrac{1}{2}a_{1}t_{3}'^{2}$

解得$t_{3}'=0.4\;\rm s$

故从小球开始运动至与槽的侧壁发生第$3$次碰撞所需的时间为

$t_{3}=t_{1}+t_{2}+t_{3}=0.2\;\rm s+0.4\;\rm s+0.4\;\rm s=1.0\;\rm s$

则以此类推，当小球第$n$次到达凹槽侧壁所用的时间为

$t_{n}=0.2\;{\rm s}+(n-1)\times 0.4\;{\rm s}=(0.4n-0.2)\;{\rm s}(n=1,2,3\cdots)$