高中 | 带电粒子在匀强电场中的偏转运动 题目答案及解析
稿件来源:高途
高中 | 带电粒子在匀强电场中的偏转运动题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
带电粒子在匀强电场中的偏转运动
如图所示的真空环境中,由$a$、$b$、$c$三个平行界面分隔出的Ⅰ、Ⅱ两个区域,宽度均为$L=0.12\;\rm m$,沿$c$界面放置足够长的荧光屏。一带电量为$q=1\times 10^{-6}\;\rm C$、质量为$m=3 \times 10^{-10}\;\rm kg$的带正电粒子从界面$a$上的$P$点以速度$v_{0}=5 \times 10^{2}\;\rm m/s$垂直界面射入区域Ⅰ。若在区域Ⅰ加上垂直纸面向外的匀强磁场,磁感应强度大小为$B=1\;\rm T$,粒子能打在荧光屏上的某一点$Q$(未画出);若在区域Ⅰ加上与界面平行的匀强电场,粒子也能击中荧光屏上的$Q$点。不计粒子重力,不计边界效应。求
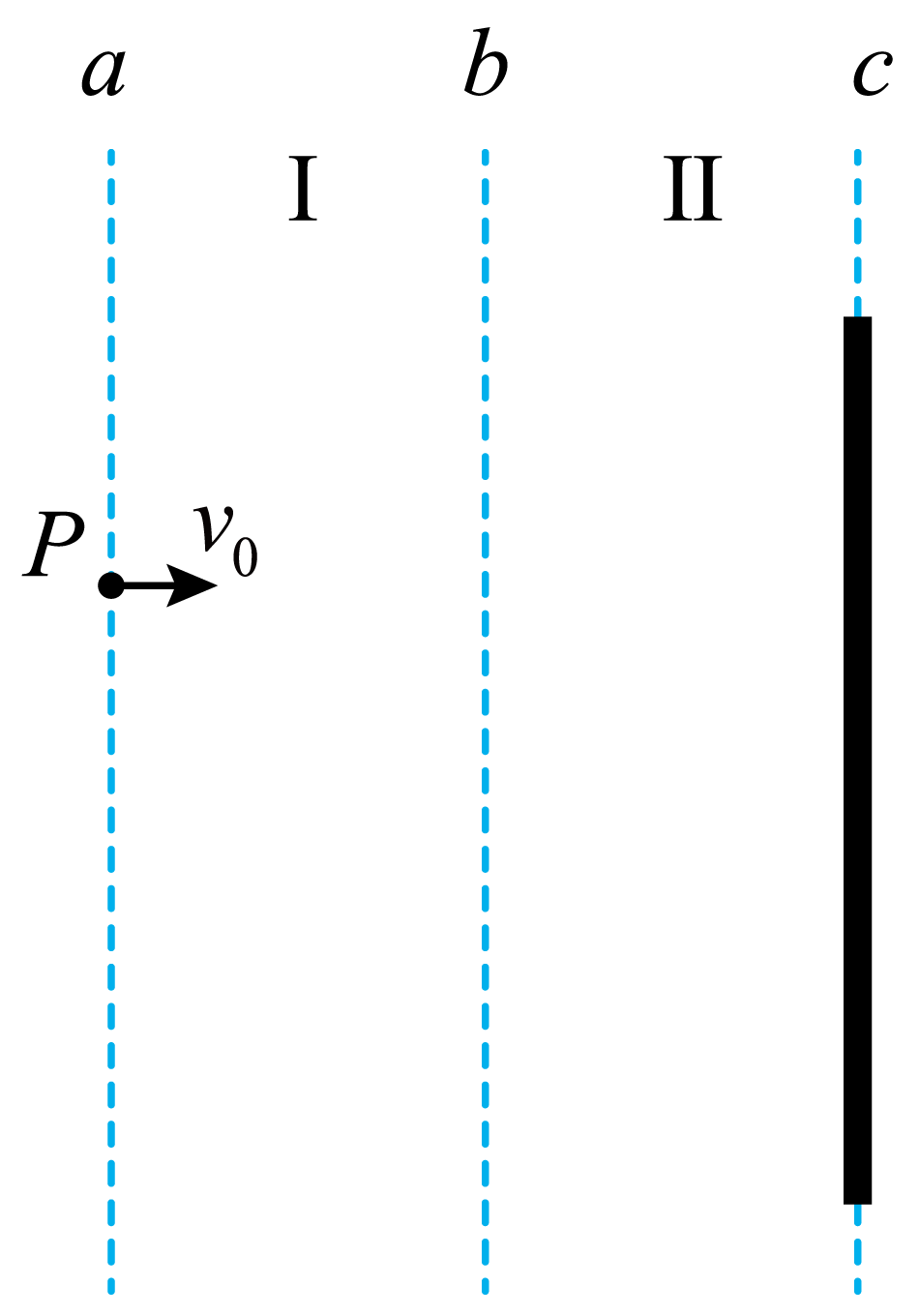
$P$与$Q$在沿界面方向上的距离$D$;
$0.22\\;\\rm m$;
"]]加磁场时,根据$qv_{0}B=\dfrac{mv_{0}^{2}}{r}$
可得$r=\dfrac{mv_{0}}{qB}=0.15\;\rm \text{m}$
粒子在区域Ⅰ中的偏移量$y_{1}'=r(1-\cos\theta)=0.06\;\rm m$
粒子在区域Ⅱ中的偏移量$y_{1}''=L\tan\theta=0.16\;\rm m$
所以,$P$与$Q$在沿界面方向上的距离$D=y_{1}'+y_{1}''=0.22\;\rm m$
电场强度$E$的大小。
$764\\;\\rm V/m$
"]]加电场时,粒子在区域Ⅰ中做类平抛运动,则$L=v_{0}t$
${y_{2}}'=\dfrac{1}{2}\dfrac{qE}{m}t^{2}=\dfrac{qEL^{2}}{2mv_{0}^{2}}$
粒子在区域Ⅱ中有做匀速直线运动,在$y$轴方向${y_{2}}''=v_{y}t=at \cdot t=\dfrac{qEL^{2}}{mv_{0}^{2}}$
仍然打在$Q$点,则$D={y_{2}}'+{y_{2}}''=\dfrac{3qEL^{2}}{2mv_{0}^{2}}=0.22\;\rm \text{m}$
解得$E=\dfrac{275}{108} \times 10^{2}=764\;\rm \text{V}/\text{m}$
高中 | 带电粒子在匀强电场中的偏转运动题目答案及解析(完整版)
