真空中有一匀强磁场，磁场边界为两个半径分别为$a$和$3a$的同轴圆柱面，磁场的方向与圆柱轴线平行，其横截面如图所示。一速率为$v$的电子从圆心沿半径方向进入磁场。已知电子质量为$m$，电荷量为$e$，忽略重力。为使该电子的运动被限制在图中实线圆围成的区域内，磁场的磁感应强度最小为$(\quad\ \ \ \ )$

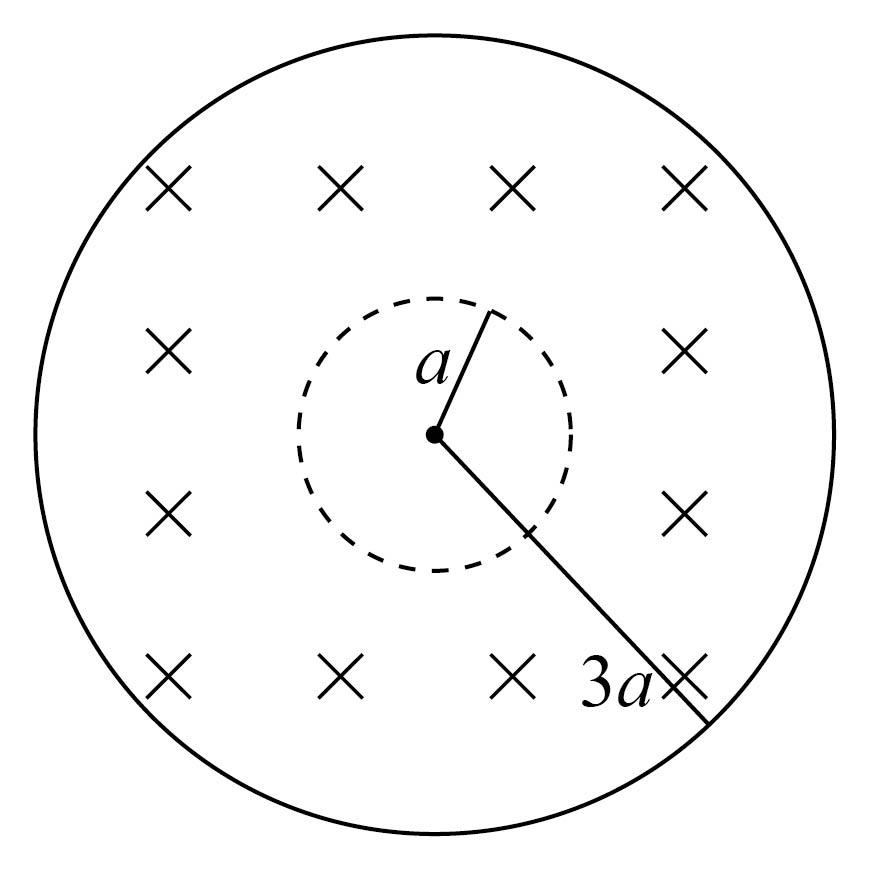
$\\dfrac{3mv}{2ae}$

$\\dfrac{mv}{ae}$

$\\dfrac{3mv}{4ae}$

$\\dfrac{3mv}{5ae}$

当电子在磁场中的运动轨迹和外圆相切时，电子在图中实线圆围成的区域内运动的半径最大，
电子的运动轨迹如图，

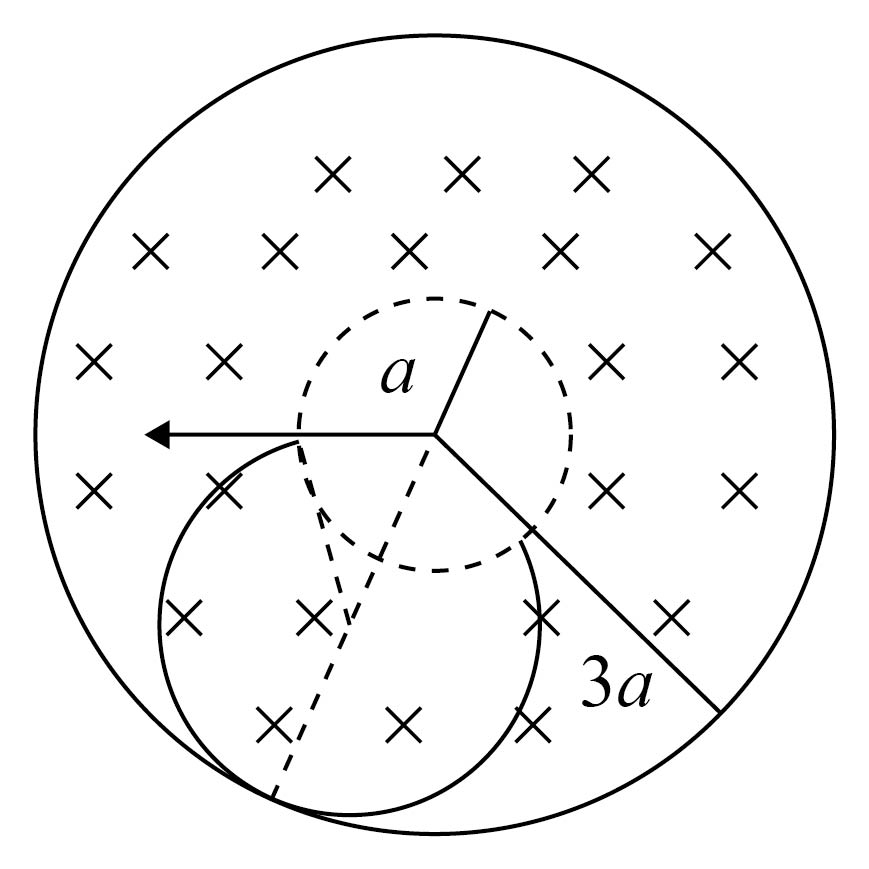
令电子的半径为$r$，根据几何知识有${{r}^{2}}+{{a}^{2}}={{(3a-r)}^{2}}$，
所以电子的最大半径为$r=\dfrac{4}{3}a$，
因为$evB=m\dfrac{{{v}^{2}}}{r}$，
所以$B=\dfrac{mv}{re}$，
则磁感应强度的最小值为$B=\dfrac{3mv}{4ae}$，故$\text{ABD}$错误，$\text{C}$正确。
故选：$\text{C}$。